Giải Toán lớp 8 bài 1: Đơn thức bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 8 Tập 1 Kết nối tri thức với cuộc sống trang 5, 6, 7, 8, 9, 10.
Lời giải Toán 8 Bài 1 Kết nối tri thức trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 8, từ đó học tốt môn Toán lớp 8 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài 1 Chương I: Đa thức. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
Toán 8 Bài 1: Đơn thức Kết nối tri thức
Giải Toán 8 Kết nối tri thức Tập 1 Bài 1 - Luyện tập
Luyện tập 1
Trong các biểu thức sau đây, biếu thức nào là đơn thức?
![]()
Bài giải:
![]()
Luyện tập 2
Thu gọn và xác định bậc của đơn thức 4,5x2y (−2) xyz
Bài giải:
4,5x2y (−2) x y z = [4.5 × (−2)] (x2 × x) (y × y) z = − 9x3y2z
Bậc của đơn thức là 6
Luyện tập 3
Cho các đơn thức:![]()
Hãy sắp xếp các đơn thức đã cho thành từng nhóm, sao cho tất cả các đơn thức đồng dạng thì cùng một nhóm.
Bài giải:
Nhóm 1: ![]()
Nhóm 2: ![]()
Nhóm 3: ![]()
Luyện tập 4
Cho các đơn thức − x3y; 4x3y và − 2x3y
a) Tính tổng S của ba đơn thức đó.
b) Tính giá trị tổng S tại x = 2; y = -3
Bài giải:
a) S = − x3y + 4x3y + − 2x3y
= (− 1 + 4 − 2) x3y = x3y
b) Thay x = 2; y = -3 vào S, ta có: S = 23 × (− 3) = − 24
Vậy S = –24 tại x = 2; y = –3.
Giải Toán 8 Kết nối tri thức Tập 1 trang 9, 10
Bài 1.1
Trong các biểu thức sau, biểu thức nào là đơn thức?
![]()
Bài giải:
![]()
Bài 1.2
Cho các đơn thức:
![]()
a) Liệt kê các đơn thức thu gọn trong các đơn thức đã cho và thu gọn các đơn thức còn lại.
b) Với mỗi đơn thức nhận được, hãy cho biết hệ số, phần biến và bậc của nó.
Bài giải:
a) Các đơn thức đã thu gọn: B, D
![]()
![]()
b) Hệ số của đơn thức A là -8, phần biến là x3y và bậc là 4
Hệ số của đơn thức B là 12,75, phần biến xyz là và bậc là 3
Hệ số của đơn thức C là 2, phần biến là x2y4 và bậc là 6
Hệ số của đơn thức A là ![]() , phần biến là x và bậc là 1
, phần biến là x và bậc là 1
Bài 1.3
Thu gọn rồi tính giá trị của mỗi đơn thức sau:
a) ![]() khi
khi ![]()
b) ![]() khi x = 4; y = 0,5; z = 2.
khi x = 4; y = 0,5; z = 2.
Bài giải:
a) ![]()
Thay ![]() vào A, ta có:
vào A, ta có:
![]()
b) ![]()
Thay x = 4; y = 0,5; z = 2 vào B ta có:
![]()
Bài 1.4
Sắp xếp các đơn thức sau thành từng nhóm, mỗi nhóm chứa tất cả các đơn thức đồng dạng với nhau:
![]()
Bài giải:
Nhóm 1: ![]()
Nhóm 2: ![]()
Nhóm 3: ![]()
Bài 1.5
Rút gọn rồi tính giá trị của biểu thức
![]() khi x = -2 và y = 1
khi x = -2 và y = 1
Bài giải:
![]()
Thay x = -2, y = 1 vào S ta có:
![]()
Bài 1.6
Tính tổng của bốn đơn thức:
![]()
Bài giải:
![]()
![]()
Bài 1.7
Một mảnh đất có dạng như phần được tô màu xanh trong hình bên cùng với các kích thước được ghi trên đó. Hãy tìm đơn thức (thu gọn) với hai biến x và y biểu thị diện tích của mảnh đất đã cho bằng hai cách:
Cách 1. Tính tổng diện tích của hai hình chữ nhật ABCD và EFGC
Cách 2. Lấy diện tích của hình chữ nhật HFGD trừ đi diện tích của hình chữ nhật HEBA
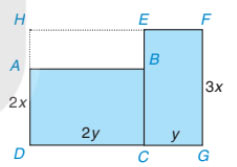
Bài giải:
Cách 1:
Diện tích hình chữ nhật ABCD: 2x × 2y = 4xy
Diện tích hình chữ nhật EFGC: 3x×y = 3xy
Diện tích mảnh đất: 4xy + 3xy = 7xy
Cách 2:
Diện tích hình chữ nhật HFGD: 3x × (2y + y) = 9xy
Diện tích hình chữ nhật HEBA: (3x − 2 x) × 2y = 2xy
Diện tích mảnh đất: 9xy - 2xy = 7xy
