Giải Toán lớp 7 Luyện tập chung bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 7 Tập 1 Kết nối tri thức với cuộc sống trang 85, 86.
Lời giải Toán 7 Kết nối tri thức trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 7, từ đó học tốt môn Toán lớp 7 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Luyện tập chung Chương IV - Tam giác bằng nhau. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
Giải Toán 7 bài Luyện tập chung trang 85 Kết nối tri thức với cuộc sống
Giải Toán 7 Kết nối tri thức với cuộc sống trang 86 tập 1
Bài 4.29
Cho Hình 4.73. Hãy tính các độ dài a, b và số đo x, y của các góc trên hình vẽ.
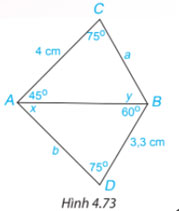
Hướng dẫn giải:
- Trường hợp 1: cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
- Trường hợp 2: cạnh – góc – cạnh: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
- Trường hợp 3: góc – cạnh – góc: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Gợi ý đáp án:
Xét tam giác ABC có:

Xét tam giác ABD có:

Xét 2 tam giác ABC và ADB có:
![]()
AB chung
![]()
![]()
=>BC=BD (2 cạnh tương ứng), mà BD = 3,3 cm =>a= BC= 3,3cm
AC=AD (2 cạnh tương ứng), mà AC = 4 cm =>b = AD = 4cm
Bài 4.30
Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM =ON, OA > OM.
Chứng minh rằng:
a) ![]() ;
;
b) ![]() .
.
Hướng dẫn giải:
- Trường hợp 1: cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
- Trường hợp 2: cạnh – góc – cạnh: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
- Trường hợp 3: góc – cạnh – góc: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Gợi ý đáp án:
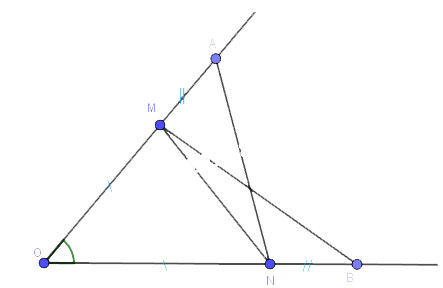
a) Xét tam giác OAN và OBM có:
OA=OB
![]() chung
chung
OM=ON
![]()
b) Do ![]() nên AN=BM (2 cạnh tương ứng);
nên AN=BM (2 cạnh tương ứng); ![]() (2 góc tương ứng)
(2 góc tương ứng) ![]()
Do OA + AM = OM; OB + BN = ON
Mà OA = OB, OM =ON
=> AM=BN
Xét hai tam giác AMN và BNM có:
AN=BM
![]()
AM=BN
![]()
Bài 4.31
Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:
a) AC = BD;
b) ![]() .
.
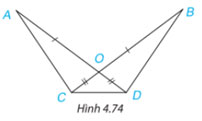
Hướng dẫn giải:
- Trường hợp 1: cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
- Trường hợp 2: cạnh – góc – cạnh: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
- Trường hợp 3: góc – cạnh – góc: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Gợi ý đáp án:
a) Ta có: OA = OB, OC = OD nên AD=BC
Do OC=OD nên tam giác OCD cân ![]()
Xét 2 tam giác ACD và BDC có:
AD=BC
![]()
CD chung
![]()
=>AC=BD (hai cạnh tương ứng)
b) Xét hai tam giác ACD và BDC có:
AO=BO
CO=DO
AC=BD
![]()
Bài 4.32
Cho tam giác MBC vuông tại M có ![]() . Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.
. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.
Hướng dẫn giải:
- Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau (cùng bằng 600)
- Tam giác cân có một góc bằng 600 là tam giác đều.
- Điểm nằm trên đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó
Gợi ý đáp án:
Xét 2 tam giác vuông CMB và CMA có:
MC chung
MB=MA
![]()
=>CA = CB (2 cạnh tương ứng).
=> Tam giác ABC cân tại C.
Mà góc B bằng 60o
=>Tam giác ABC đều.
