Giải Toán lớp 7 trang 51 tập 1 Cánh diều giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời câu hỏi luyện tập và 6 bài tập cuối bài trong SGK bài 4 Làm tròn và ước lượng.

Toán 7 Cánh diều tập 1 trang 51 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán lớp 7 tập 1. Giải Toán 7 Làm tròn và ước lượng là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.

Giải Luyện tập Toán 7 Bài 4 Cánh Diều

Luyện tập 1

Khoảng cách từ sân vận động Old Traford ở Greater Manchester đến tháp đồng hood Big Ben ở London (Vương quốc Anh) là 201 dặm. (Nguồn: https://ww.google.com) Tính khoảng cách đó theo đơn vị Ki – lô – mét (làm tròn đến hàng đơn vị), biết 1 dặm = 1,609344)

Gợi ý đáp án 

Khoảng cách từ sân vận động Old Traford ở Greater Manchester đến tháp đồng hood Big Ben ở London (Vương quốc Anh) tính theo đơn vị ki – lô – mét là:

201 . 1,609344 km = 323,478144 km ≈ 323,5 km

Luyện tập 2

a) Làm tròn số 23 615 với độ chính xác 5.

b) Làm tròn số 187 638 với độ chính xác 50.

Gợi ý đáp án

Thực hiện các phép tính như sau:

a) Làm tròn số 23 615 với độ chính xác 5.

=> Để làm tròn số trên đến 5 ta sẽ làm tròn đến hàng chục

Gạch chân dưới chữ số hàng chục 23 615

Nhận thấy chữ số ở hàng đơn vị là 5 nên ta tăng thêm chữ số hàng chục một đơn vị. Phần các chữ số đằng sau ta thay bằng số 0

=> Làm tròn số 23 615 với độ chính xác 5 ta được kết quả bằng 23 620

b) Làm tròn số 187 638 với độ chính xác 50.

=> Để làm tròn số trên đến 50 ta sẽ làm tròn đến hàng trăm

Gạch chân dưới chữ số hàng trăm 187 638

Nhận thấy chữ số ở hàng chục là 3 < 5 nên ta giữ nguyên chữ số hàng trăm. Phần các chữ số đằng sau ta thay bằng số 0

=> Làm tròn số 23 615 với độ chính xác 5 ta được kết quả bằng 187 600

Giải Toán 7 trang 51 Cánh diều Tập 1

Bài 1

Làm tròn số 98 176 244 với độ chính xác là 5 000.

Gợi ý đáp án

Vì 1 000 < 5 000 < 10 000 nên ta làm tròn số 98 176 244 đến hàng mười nghìn.

Gạch chân dưới chữ số hàng mười nghìn: 98 176 244.

Nhận thấy chữ số hàng nghìn là 6 > 5 nên ta tăng thêm chữ số hàng mười nghìn một đơn vị và thay các chữ số hàng nghìn, hàng trăm, hàng chục và hàng đơn vị bởi số 0.

Khi đó số 98 176 244 làm tròn đến hàng mười nghìn ta thu được kết quả là 98 180 000.

Vậy số 98 176 244 làm tròn với độ chính xác 5000 ta thu được kết quả là 98 180 000.

Bài 2

a) Làm tròn số 4,76908 với độ chính xác 0,5.

b) Làm tròn số –4,76908 với độ chính xác 0,05.

Gợi ý đáp án

a) Vì 0,1 < 0,5 < 1 nên ta sẽ làm tròn số 4,76908 đến hàng đơn vị.

Gạch chân dưới chữ số hàng đơn vị 4,76908.

Nhận thấy chữ số ở hàng phần mười là 7 > 5 nên ta tăng thêm chữ số hàng đơn vị một đơn vị. Phần các chữ số đằng sau hàng đơn vị là phần thập phân nên ta bỏ đi.

Khi đó, số 4,76908 làm tròn đến hàng đơn vị ta thu được kết quả là 5.

Vậy số 4,76908 làm tròn với độ chính xác là 0,5 ta thu được kết quả là 5.

b) Vì 0,01 < 0,05 < 0,1 nên ta sẽ làm tròn số –4,76908 đến hàng phần mười.

Gạch chân dưới chữ số hàng phần mười –4,76908.

Nhận thấy chữ số ở hàng phần trăm là 6 > 5 nên ta tăng thêm chữ số hàng phần mười một đơn vị. Phần các chữ số đằng sau hàng phần mười ta bỏ đi.

Khi đó, số –4,76908 làm tròn đến hàng phần mười ta thu được kết quả là –4,8.

Vậy số –4,76908 làm tròn với độ chính xác là 0,05 ta thu được kết quả là –4,8.

Bài 3

a) Sử dụng máy tính cầm tay để tính rồi viết mỗi số sau dưới dạng số thập phân vô hạn (tuần hoàn hoặc không tuần hoàn):

b) Làm tròn số với độ chính xác 0,05.

Gợi ý đáp án

a)

b) Làm tròn số với độ chính xác 0,05, tức là làm tròn số -4,3588989… đến chữ số hàng phần trăm, ta được -4,36

Bài 4

Áp dụng quy tắc làm tròn số để ước lượng kết quả của mỗi phép tính sau:

a) (–28,29) + (–11,91)

b) 43,91 – 4,49

c) 60,49.(–19,51)

a) (–28,29) + (–11,91)

Gợi ý đáp án

Làm tròn số –28,29 đến hàng đơn vị ta được số –28; làm tròn số –11,91 đến hàng đơn vị ta được số –12.

Khi đó kết quả phép tính của hai số đã làm tròn là (–28) + (–12) = –40.

Vậy kết quả của phép tính (–28,29) + (–11,91) gần với –40.

b) 43,91 – 4,49

Làm tròn số 43,91 đến hàng phần mười ta được số 43,9; làm tròn số 4,49 đến hàng phần mười ta được số 4,5.

Khi đó kết quả phép tính hai số đã làm tròn là: 43,9 – 4,5 = 39,4.

Vậy kết quả của phép tính 43,91 – 4,5 gần với 39,4.

c) 60,49.(–19,51)

Làm tròn số 60,49 đến hàng đơn vị ta được số 60; làm tròn số –19,51 đến hàng đơn vị ta được số –20.

Khi đó kết quả phép tính hai số đã làm tròn là: 60.(–20) = –1200.

Vậy kết quả của phép tính 60,49.(–19,51) gần với –1200.

Bài 5

Các nhà khoa học tính được vận tốc ánh sáng bằng 299 792 458 m/s. Để dễ nhớ, người ta nói vận tốc ánh sáng là 300 000 000 m/s. Số liệu đó đã được làm tròn đến hàng nào?

Gợi ý đáp án

Độ chính xác d là:

300 000 000 – 299 792 458 = 207 542

Vì 100 000 < 207 542 < 500 000 nên số liệu đã được làm tròn đến hàng triệu.

Bài 6

Đề bài

Thống kê diện tích và dân số ngày 01/4/2019 của một số vùng ở Việt Nam như sau:

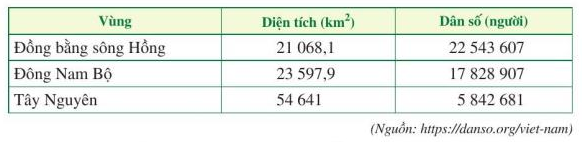
Căn cứ vào bảng thống kê trên, tính mật độ dân số của các vùng nói trên (làm tròn kết quả đến hàng đơn vị), biết rằng: “Mật độ dân số vùng (người/ km²) là tỉ số giữa dân số và diện tích của vùng đó.”

Gợi ý đáp án

Mật độ dân số của vùng:

+ Đồng bằng sông Hồng là:  (người/km²)

+ Đông Nam Bộ là: (người/km²)

+ Tây Nguyên là:  (người/km²)