Giải Toán 7 trang 46 Kết nối tri thức với cuộc sống

Giải Toán lớp 7 bài 9: Hai đường thẳng song song và dấu hiệu nhận biết bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 7 Tập 1 Kết nối tri thức với cuộc sống trang 46, 47, 48, 49.

Lời giải Toán 7 Bài 9 Kết nối tri thức trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 7, từ đó học tốt môn Toán lớp 7 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài 9 Chương III - Góc và đường thẳng song song. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Giải Toán 7 bài 9: Hai đường thẳng song song và dấu hiệu nhận biết sách Kết nối tri thức với cuộc sống

Giải Toán 7 Kết nối tri thức tập 1 Bài 9 - Luyện tập
- Luyện tập 1
- Luyện tập 2
Giải Toán 7 Kết nối tri thức với cuộc sống trang 49 tập 1

Giải Toán 7 Kết nối tri thức tập 1 Bài 9 - Luyện tập

Luyện tập 1

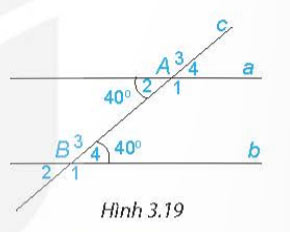
Quan sát hình 3.19:

a) Biết $\widehat {{A_2}} = {40^0},\widehat {{B_4}} = {40^0}$ . Em hãy cho biết số đo các góc còn lại.

b) Các cặp góc A₁ và B₄; A₂ và B₃ được gọi là các cặp góc trong cùng phía. Tính tổng $\widehat {{A_1}} + \widehat {{B_4}},\widehat {{A_2}} + \widehat {{B_3}}$

Hình 3.19

Gợi ý đáp án:

a) Ta có: Góc A₁ và góc A₂ là hai góc kề bù

Suy ra: $\widehat {{A_1}} + \widehat {{A_2}} = {180^0} \Rightarrow \widehat {{A_1}} = {180^0} - \widehat {{A_2}} = {180^0} - {40^0} = {140^0}$

Góc A₂ và góc A₄ là hai góc đối đỉnh

Suy ra: $\widehat {{A_2}} = \widehat {{A_4}} = {40^0}$

Góc A₁ và góc A₃ là hai góc đối đỉnh

Suy ra: $\widehat {{A_1}} = \widehat {{A_3}} = {140^0}$

Ta có: Góc B₁ và góc B₄ là hai góc kề bù

Suy ra: $\widehat {{B_1}} + \widehat {{B_4}} = {180^0} \Rightarrow \widehat {{B_1}} = {180^0} - \widehat {{B_4}} = {180^0} - {40^0} = {140^0}$

Góc B₂ và góc B₄ là hai góc đối đỉnh

Suy ra: $\widehat {{B_2}} = \widehat {{B_4}} = {40^0}$

Góc B₁ và góc B₃ là hai góc đối đỉnh

Suy ra: $\widehat {{B_1}} = \widehat {{B_3}} = {140^0}$

b) Ta có:

$\begin{matrix} \widehat {{A_1}} + \widehat {{B_4}} = {140^0} + {40^0} = {180^0} \hfill \\ \widehat {{A_2}} + \widehat {{B_3}} = {40^0} + {140^0} = {180^0} \hfill \\ \end{matrix}$

Luyện tập 2

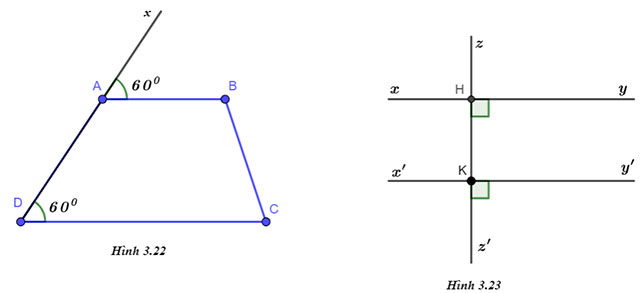
1) Quan sát Hình 3.22 và giải thích tại sao AB // DC.

2) Tìm trên hình 3.23 hai đường thẳng song song với nhau và giải thích vì sao chúng song song.

Hình 3.22, 3.23

Gợi ý đáp án:

1) Quan sát hình 3.22 ta có:

$\widehat {xAB} = {60^0},\widehat {ADC} = {60^0}$

Mà hai góc $\widehat {xAB},\widehat {ADC}$ nằm ở vị trí so le trong

=> AB // DC

2) Quan sát hình 3.23 ta có:

xx' vuông góc với zz’ => $\widehat {zHy} = {90^0}$

yy’ vuông góc với zz’ => $\widehat {HKy'} = {90^0}$

=> $\widehat {zHy} = \widehat {HKy'} = {90^0}$

Mặt khác hai góc $\widehat {zHy},\widehat {HKy'}$ nằm ở vị trí đồng vị.

Suy ra xx’ // yy’

Giải Toán 7 Kết nối tri thức với cuộc sống trang 49 tập 1

Bài 3.6

Quan sát Hình 3.24.

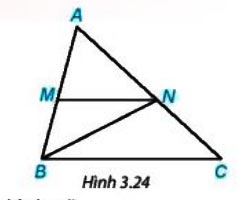
Hình 3.24

a) Tìm một góc ở vị trí so le trong với góc MNB.

b) Tìm một góc ở vị trí đồng vị với góc ACB.

c) Kể tên một cặp góc trong cùng phía.

d) Biết MN // BC, em hãy kể tên ba cặp góc bằng nhau trong hình vẽ.

Gợi ý đáp án:

a) Góc ở vị trí so le trong với góc MNB là góc NBC.

b) Góc ở vị trí đồng vị với góc ACB là góc ANM.

c) Cặp góc trong cùng phía là: góc MNB và góc MBC

d) Ta có: MN // BC

=> $\widehat {AMN} = \widehat {ABC}$ (Hai góc đồng vị)

=> $\widehat {ANM} = \widehat {ACB}$ (Hai góc đồng vị)

=> $\widehat {MNB} = \widehat {NBC}$ (Hai góc so le trong)

Bài 3.7

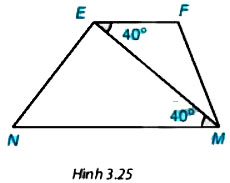
Quan sát Hình 3.25. Biết . Em hãy giải thích tại sao EF // NM.

Hình 3.25

Gợi ý đáp án:

Theo bài ra ta có:

$\widehat {MEF} = {40^0},\widehat {EMN} = {40^0}$

Mà hai góc $\widehat {MEF},\widehat {EMN}$ nằm ở vị trí so le trong

=> EF // NM

Bài 3.8

Quan sát hình 3.26, giải thích tại sao AB // DC.

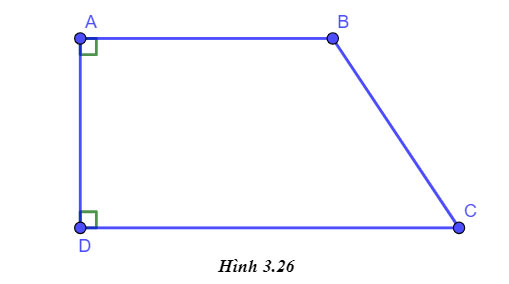
Hình 3.26

Gợi ý đáp án:

Ta có:

AB vuông góc với AD => $\widehat {DAB} = {90^0}$

CD vuông góc với AD => $\widehat {ADC} = {90^0}$

=> $\widehat {DAB} = \widehat {ADC} = {90^0}$

Mặt khác hai góc $\widehat {DAB},\widehat {ADC}$ nằm ở vị trí đồng vị.

Suy ra AB // CD

Bài 3.9

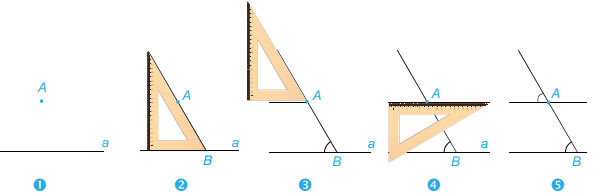
Cho điểm A và đường thẳng d không đi qua A. Hãy vẽ đường thẳng d’ đi qua A và song song với d.

Gợi ý đáp án:

Dùng góc nhọn 60⁰ của ê ke

Bài 3.9

Bài 3.10

Cho hai điểm A và B. Hãy vẽ đường thẳng a đi qua A và đường thẳng b đi qua B sao cho a song song với b.

Gợi ý đáp án:

Vẽ đường thẳng b bất kì đi qua điểm B rồi vẽ đường thẳng a đi qua A và song song với b như bài tập 3.9

Bài 3.9

Bài 3.11

Hãy vẽ hai đoạn thẳng AB và MN sao cho AB // MN và AB = MN.

Gợi ý đáp án:

Ta thực hiện theo các bước như sau:

Bước 1. Vẽ đoạn thẳng AB (giả sử AB = 3cm).

Bước 2. Lấy điểm M nằm ngoài đoạn thẳng AB.

Bước 3. Vẽ đường thẳng qua M song song với đoạn thẳng AB. Trên đường thẳng này lấy điểm N sao cho MN = 3cm. Khi đó MN = AB = 3cm.

Ta có hình vẽ như sau:

Bài 3.11

Giải Toán 7 trang 46 Kết nối tri thức với cuộc sống - Tập 1

Toán 7 Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết

Giải Toán lớp 7 trang 46 - Tập 1 sách Kết nối tri thức với cuộc sống

Giải Toán 7 bài 9: Hai đường thẳng song song và dấu hiệu nhận biết sách Kết nối tri thức với cuộc sống

Giải Toán 7 Kết nối tri thức tập 1 Bài 9 - Luyện tập

Luyện tập 1

Luyện tập 2

Giải Toán 7 Kết nối tri thức với cuộc sống trang 49 tập 1

Bài 3.6

Bài 3.7

Bài 3.8

Bài 3.9

Bài 3.10

Bài 3.11

Liên kết tải về

Chủ đề liên quan

Học tập

Lớp 7

Toán 7 Kết nối tri thức

Chia sẻ

Có thể bạn quan tâm

Được tải nhiều nhất

Bài viết mới nhất