Giải Toán lớp 7 Bài tập cuối chương 1 bao gồm đáp án chi tiết, cùng hướng dẫn giải các bài tập trong SGK Toán 7 Tập 1 Chân trời sáng tạo trang 27, 28.
Lời giải Toán 7 Chân trời sáng tạo trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 7, từ đó học tốt môn Toán lớp 7 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài tập cuối chương I - Số hữu tỉ. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
Giải Toán 7 Bài tập cuối chương 1 Chân trời sáng tạo
Giải Toán 7 Chân trời sáng tạo trang 27, 28 tập 1
Bài 1
Thực hiện phép tính.
![]()


![]()
Hướng dẫn giải:
Theo quy tắc chuyển vế, ta có thể phát biểu như sau:
- Khi chuyển một số hạng trong một đẳng thức từ vế này sang vế kia. Ta phải đổi dấu số hạng đó. Nếu số hạng là số nguyên dương, ta đổi dấu cộng thành dấu trừ.
- Và ngược lại, nếu số hạng là số nguyên âm, ta đổi dấu trừ thành dấu cộng.
Gợi ý đáp án:
a) ![]()

b) 

c) 

d) ![]()
![\begin{matrix}
= \left( { - \dfrac{3}{4}} \right) - \left[ {\left( { - 2} \right) + \dfrac{3}{2}} \right]:\dfrac{3}{2} - \dfrac{5}{4} \hfill \\
= \left( { - \dfrac{3}{4}} \right) - \left[ {\dfrac{{ - 4}}{2} + \dfrac{3}{2}} \right]:\dfrac{3}{2} - \dfrac{5}{4} \hfill \\
= \left( { - \dfrac{3}{4}} \right) - \left( { - \dfrac{1}{2}} \right):\dfrac{3}{2} - \dfrac{5}{4} \hfill \\
\end{matrix}](https://o.rada.vn/data/image/holder.png)
![\begin{matrix}
= \left( { - \dfrac{3}{4}} \right) - \left( { - \dfrac{1}{2}} \right).\dfrac{2}{3} - \dfrac{5}{4} \hfill \\
= \left( { - \dfrac{3}{4}} \right) - \left( {\dfrac{{ - 1}}{3}} \right) - \dfrac{5}{4} \hfill \\
= \left[ { - \dfrac{3}{4} - \dfrac{5}{4}} \right] + \dfrac{1}{3} \hfill \\
= \dfrac{{ - 8}}{4} + \dfrac{1}{3} = - 2 + \dfrac{1}{3} = \dfrac{{ - 5}}{3} \hfill \\
\end{matrix}](https://o.rada.vn/data/image/holder.png)
Bài 2
Thực hiện phép tính (bằng cách hợp lí nếu có thể).
![]()
![]()
![]()
![]()
Hướng dẫn giải:
Theo quy tắc chuyển vế, ta có thể phát biểu như sau:
- Khi chuyển một số hạng trong một đẳng thức từ vế này sang vế kia. Ta phải đổi dấu số hạng đó. Nếu số hạng là số nguyên dương, ta đổi dấu cộng thành dấu trừ.
- Và ngược lại, nếu số hạng là số nguyên âm, ta đổi dấu trừ thành dấu cộng.
Gợi ý đáp án:
a) ![]()

b) ![]()

c) ![]()

d) ![]()

Bài 3
Thực hiện phép tính.
![]()
![]()
![]()
Hướng dẫn giải:
Theo quy tắc chuyển vế, ta có thể phát biểu như sau:
- Khi chuyển một số hạng trong một đẳng thức từ vế này sang vế kia. Ta phải đổi dấu số hạng đó. Nếu số hạng là số nguyên dương, ta đổi dấu cộng thành dấu trừ.
- Và ngược lại, nếu số hạng là số nguyên âm, ta đổi dấu trừ thành dấu cộng.
Gợi ý đáp án:
Thực hiện các phép tính như sau:
a) 
b) ![]()

c) ![]()

Bài 4
Tính giá trị các biểu thức sau:
![]()
![]()
Hướng dẫn giải:
Theo quy tắc chuyển vế, ta có thể phát biểu như sau:
- Khi chuyển một số hạng trong một đẳng thức từ vế này sang vế kia. Ta phải đổi dấu số hạng đó. Nếu số hạng là số nguyên dương, ta đổi dấu cộng thành dấu trừ.
- Và ngược lại, nếu số hạng là số nguyên âm, ta đổi dấu trừ thành dấu cộng.
Gợi ý đáp án:
a) ![]()
![\begin{matrix}
A = \left[ {\left( { - \dfrac{1}{2}} \right) - \dfrac{3}{5}} \right]:\left( { - 3} \right) + \dfrac{1}{3} - \dfrac{1}{6}:2 \hfill \\
A = \left[ {\left( { - \dfrac{5}{{10}}} \right) - \dfrac{6}{{10}}} \right].\left( {\dfrac{{ - 1}}{3}} \right) + \dfrac{1}{3} - \dfrac{1}{6}.\dfrac{1}{2} \hfill \\
A = \left( {\dfrac{{ - 11}}{{10}}} \right).\left( {\dfrac{{ - 1}}{3}} \right) + \dfrac{1}{3} - \dfrac{1}{{12}} \hfill \\
A = \dfrac{{11}}{{30}} + \dfrac{1}{3} - \dfrac{1}{{12}} \hfill \\
A = \dfrac{{22}}{{60}} + \dfrac{{20}}{{60}} - \dfrac{5}{{60}} = \dfrac{{37}}{{60}} \hfill \\
\end{matrix}](https://o.rada.vn/data/image/holder.png)
b) ![]()
![\begin{matrix}
B = \left( {\dfrac{2}{{25}} - \dfrac{9}{{250}}} \right):\dfrac{{11}}{{50}} - \left[ {\left( {\dfrac{{13}}{4} - \dfrac{{22}}{9}} \right)} \right].\dfrac{9}{{29}} \hfill \\
B = \left( {\dfrac{{20}}{{250}} - \dfrac{9}{{250}}} \right):\dfrac{{11}}{{50}} - \left[ {\left( {\dfrac{{117}}{{36}} - \dfrac{{88}}{{36}}} \right)} \right].\dfrac{9}{{29}} \hfill \\
B = \dfrac{{11}}{{250}}:\dfrac{{11}}{{50}} - \dfrac{{29}}{{36}}.\dfrac{9}{{29}} \hfill \\
B = \dfrac{{11}}{{250}}.\dfrac{{50}}{{11}} - \dfrac{{29}}{{36}}.\dfrac{9}{{29}} \hfill \\
B = \dfrac{1}{5} - \dfrac{1}{4} = \dfrac{4}{{20}} - \dfrac{5}{{20}} = \dfrac{{ - 1}}{{20}} \hfill \\
\end{matrix}](https://o.rada.vn/data/image/holder.png)
Bài 5
Tìm x, biết:
![]()
![]()
![]()
![]()
![]()
![]()
Hướng dẫn giải:
Theo quy tắc chuyển vế, ta có thể phát biểu như sau:
- Khi chuyển một số hạng trong một đẳng thức từ vế này sang vế kia. Ta phải đổi dấu số hạng đó. Nếu số hạng là số nguyên dương, ta đổi dấu cộng thành dấu trừ.
- Và ngược lại, nếu số hạng là số nguyên âm, ta đổi dấu trừ thành dấu cộng.
Gợi ý đáp án:
a) ![]()

Vậy giá trị x cần tìm là ![]()
b) ![]()

Vậy giá trị x cần tìm là: ![]()
c) ![]()

Vậy giá trị x cần tìm là: x = 6
d) ![]()

Vậy giá trị x cần tìm là: ![]()
e) ![]()


Vậy giá trị x cần tìm là: ![]()
g) ![]()


Vậy giá trị x cần tìm là: ![]() hoặc
hoặc ![]()
Bài 6
a) Tính diện tích hình thang ABCD có các kích thước như hình sau:
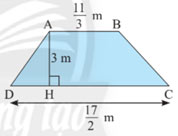
b) Hình thoi MNPQ có diện tích bằng diện tích hình thang ABCD ở câu a, đường chéo ![]() . Tính độ dài NQ.
. Tính độ dài NQ.
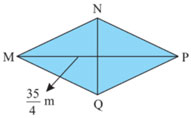
Gợi ý đáp án:
a) Diện tích hình thang là:
![]()
b) Ta có diện tích hình thoi MNPQ là ![]()
Nên ta có:

Vậy ![]()
Bài 7
Tìm số hữu tỉ a, biết rằng lấy a nhân với ![]() rồi cộng với
rồi cộng với ![]() , sau đó chia kết quả cho
, sau đó chia kết quả cho ![]() thì được số
thì được số ![]() .
.
Hướng dẫn giải
- Thứ tự thực hiện các phép tính trong một biểu thức không có dấu ngoặc
- Nếu biểu thức chỉ có phép cộng, trừ hoặc chỉ có nhân, chia ta thực hiện phép tính theo thứ tự từ trái qua phải.
- Nếu biểu thức có các phép cộng, trừ, nhân, chia, nâng lên lũy thừa ta thực hiện
Lũy thừa -> Nhân và chia -> Cộng và trừ
- Thứ tự thực hiện các phép tính đối với biểu thức có dấu ngoặc:
( ) -> [ ] -> { }
Gợi ý đáp án:
Ta có:
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Vậy ![]() .
.
Chú ý: Khi lấy kết quả chia cho ![]() ta phải để dấu ngoặc.
ta phải để dấu ngoặc.
Bài 8
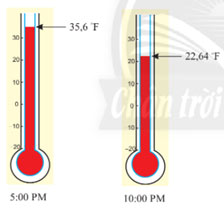
Nhiệt độ ngoài trời đo được vào một ngày mùa đông tại New York (Mĩ) lúc 5 giờ chiều là 35,6 °F, lúc 10 giờ tối cùng ngày là 22,64 °F (theo: https://www.accuweatther.com).
Biết công thức chuyển đổi từ độ F sang độ C là: ![]()
a) Hãy chuyển đổi các số đo nhiệt độ theo độ F nêu ở trên sang độ C.
b) Tính độ chênh lệch nhiệt độ từ 5 giờ chiều đến 10 giờ tối (theo đơn vị độ C).
Gợi ý đáp án:
a) Nhiệt độ tại New York (Mĩ) lúc 5h chiều là:
![]()
Nhiệt độ tại New York (Mĩ) lúc 10h tối là:
![]()
b) Độ chênh lệch nhiệt độ từ 5 giờ chiều đến 10 giờ tối là:
![]()
Vậy từ nhiệt độ lúc 5h chiều giảm 7,2 độ C so với nhiệt độ lúc 10h tối.
Bài 9
Mẹ bạn Minh gửi tiết kiệm 300 000 000 đồng vào một ngân hàng theo thể thức kì hạn 1 năm. Hết thời
hạn 1 năm, mẹ bạn Minh nhận được cả vốn lẫn lãi là 321 600 000 đồng. Tính lãi suất ngân hàng theo thể thức gửi tiết kiệm này.
Gợi ý đáp án:
Số tiền lãi mẹ bạn Minh nhận được là:
![]() (đồng)
(đồng)
Lãi suất ngân hàng là:
![]()
Bài 10
Bác Thu mua ba món hàng ở một siêu thị: Món hàng thứ nhất giá 125 000 đồng và được giảm giá 30%; món hàng thứ hai giá 300 000 đồng và được giảm giá 15%; món hàng thứ ba được giảm giá 40%. Tổng số tiền bác Thu phải thanh toán là 692 500 đồng. Hỏi giá tiền món hàng thứ ba lúc chưa giảm giá là bao nhiêu?
Gợi ý đáp án:
Món hàng thứ nhất sau khi giảm có giá là:
![]() (đồng)
(đồng)
Món hàng thứ hai sau khi giảm có giá là:
![]() (đồng)
(đồng)
Giá tiền món hàng thứ ba khi đã giảm là:
692 500 – 87 000 – 255 000 = 35 050 (đồng)
Giá tiền món hàng thứ ba khi chưa giảm là:
![]() (đồng)
(đồng)
Bài 11
Nhân ngày 30/4, một cửa hàng thời trang giảm giá 20% cho tất cả các sản phẩm. Đặc biệt nếu khách hàng nào có thẻ khách hàng thân thiết của cửa hàng thì được giảm giá thêm 10% trên giá đã giảm.
a) Chị Thanh là khách hàng thân thiết của cửa hàng, chị đã đến cửa hàng mua một chiếc váy có giá niêm yết là 800 000 đồng. Hỏi chị Thanh phải trả bao nhiêu tiền cho chiếc váy đó?
b) Cô Minh cũng là một khách hàng thân thiết của cửa hàng, cô đã mua một chiếc túi xách và đã phải trả số tiền là 864 000 đồng. Hỏi giá ban đầu của chiếc túi xách đó là bao nhiêu?
Gợi ý đáp án:
a) Vì theo như chương trình giảm 20% nhân ngày 30/4 nên giá chiếc váy chị Thanh mua sau khi giảm theo chương trình này sẽ bằng 80% giá niêm yết. Khi đó, giá chiếc váy là:
800000 . 80% = 800000 . 80 : 100 = 640000 (đồng)
Do chị Thanh là khách hàng thân thiết của cửa hàng nên được giảm thêm 10% trên giá đã giảm, vậy số tiền chị Thanh cần trả cho chiếc váy sẽ bằng 90% giá đã giảm.
Số tiền mà chị Thanh cần trả cho chiếc váy là:
640000 . 90 % = 640000.90 : 100 = 576000 (đồng)
Vậy số tiền chị Thanh cần trả cho chiếc váy là 576000 (đồng).
b) Số tiền cô Minh phải trả khi chưa dùng thẻ khác hàng thân thiết là:
864 000 : 90% = 960 000 (đồng)
Giá ban đầu của chiếc túi xách (khi chưa giảm giá dịp 30/4) là
960 000 : 80% = 1 200 000 (đồng)
Vậy giá ban đầu của chiếc túi xách là 1 200 000 đồng.
