Giải Toán lớp 6 Bài 3: Vai trò của tính đối xứng trong thế giới tự nhiên bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 6 Tập 2 Chân trời sáng tạo trang 59, 60, 61.
Lời giải Toán 6 Bài 3 Chân trời sáng tạo trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 6, từ đó học tốt môn Toán lớp 6 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài 3 Chương 7: Hình học trực quan - Tính đối xứng của hình học phẳng trong thế giới tự nhiên. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
Giải Toán 6 bài 3: Vai trò của tính đối xứng trong thế giới tự nhiên
- Giải Toán 6 Chân trời sáng tạo Thực hành
- Giải Toán 6 Chân trời sáng tạo trang 61 tập 2
- Lý thuyết Vai trò của tính đối xứng trong thế giới tự nhiên
Giải Toán 6 Chân trời sáng tạo Thực hành
Thực hành 1
Tìm hai bức ảnh về động vật, hai bức ảnh về thực vật có tính đối xứng.
Gợi ý đáp án:
* Hai bức ảnh về động vật có tính đối xứng:
- Hoa lưu ly có tính đối xứng (đối xứng trục).

- Lá trầu có tính đối xứng (đối xứng trục).

* Hai bức ảnh về thực vật có tính đối xứng:
- Con sao biển có tính đối xứng (đối xứng trục).

Con bọ rùa có tính đối xứng (đối xứng trục).

Thực hành 2
Hãy so sánh sự giống nhau về hình dạng và tính năng của con chuồn chuồn và chiếc máy bay trong hai hình dưới đây:

Gợi ý đáp án:
Sự giống nhau về hình dạng và tính năng của con chuồn chuồn và chiếc máy bay trong hai hình trên là:
Về hình dạng: Con chuồn chuồn và chiếc máy bay đều có trục đối xứng là đường thẳng nối đầu máy bay (đầu con chuồn chuồn) tới đuôi máy bay (đuôi con chuồn chuồn).
Hình minh họa:


Về tính năng: Con chuồn chuồn và chiếc máy bay đều bay được.
Thực hành 3
Tìm một số hình ảnh có tính đối xứng trong kiến trúc và hội hoạ.
Gợi ý đáp án:
Một số hình ảnh có tính đối xứng trong kiến trúc và hội hoạ như sau:
- Tháp Phước Duyên ở chùa Thiên Mụ (Huế).

- Kiến trúc Phục Hưng (kiến trúc thời kỳ giữa thế kỷ XIV - đầu thế kỷ XVII ở các vùng châu Âu).

- Ngói úp nóc mái, gắn lá đề trang trí chim phượng (thời Lý).

Giải Toán 6 Chân trời sáng tạo trang 61 tập 2
Bài 1
Hình hai chiếc lá và hình bông hoa sau đây, hình nào có trục đối xứng?
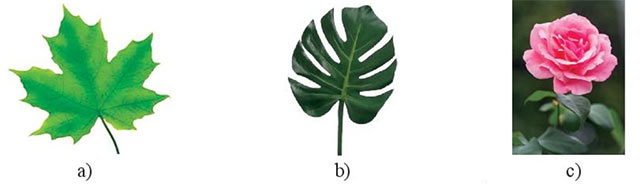
Gợi ý đáp án:
Hình a có trục đối xứng:
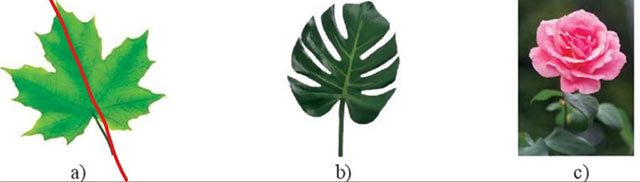
Bài 2
Hình con công và hình bông hoa sau đây, hình nào có tâm đối xứng?

Gợi ý đáp án:
Hình a) không có tâm đối xứng.
Hình b) có tâm đối xứng (như hình vẽ).

Bài 3
Hãy tìm một số hình ảnh, đồ vật trong tự nhiên có tính đối xứng (có trục đối xứng hoặc có tâm đối xứng).
Gợi ý đáp án:
- Biển báo giao thông có trục đối xứng.

- Viên gạch hoa vừa có trục đối xứng vừa có tâm đối xứng.

- Cái cốc đựng nước có trục đối xứng.

Bài 4
Nêu một số hình ảnh có tính đối xứng trong hình học.
Gợi ý đáp án:
| Hình | Trục đối xứng | Tâm đối xứng |
| Hình chữ nhật | Hai trục đối xứng là đường nối hai trung điểm của hai cạnh đối diện | Giao của hai đường chéo |
| Hình thang | Không có | Không có |
| Hình bình hành | Không có | Giao điểm của hai đường chéo |
| Hình thoi | Hai trục đối xứng là hai đường chéo | Giao điểm của hai đường chéo |
| Hình vuông | Bốn trục đối xứng | Giao điểm của hai đường chéo |
| Hình tròn | Có vô số trục đối xứng | Tâm đường tròn |
| Hình lục giác đều | Sáu trục đối xứng | Giao điểm của ba đường chéo chính |
Hình vẽ minh họa:
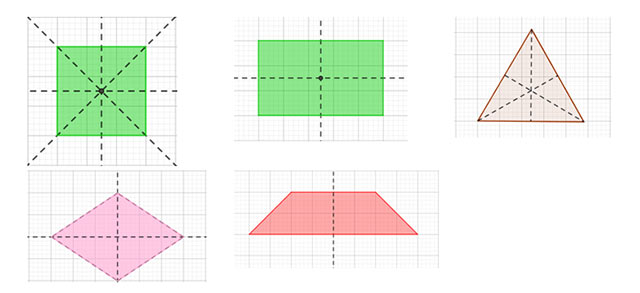
Bài 5
Tìm một số hình ảnh có tính đối xứng trong thiết bị, đồ dùng hằng ngày.
Gợi ý đáp án:
Một số hình ảnh có tính đối xứng trong thiết bị, đồ dùng hằng ngày.
Ví dụ:
- Cái cúp có trục đối xứng, không có tâm đối xứng.

- Cái đĩa vừa có trục đối xứng vừa có tâm đối xứng.

- Cái bảng vừa có trục đối xứng vừa có tâm đối xứng.

Lý thuyết Vai trò của tính đối xứng trong thế giới tự nhiên
1. Tính đối xứng trong tự nhiên
Tính đối xứng có vai trò quan trọng trong tự nhiên:
- Tính đối xứng của một đối tượng là một trong những dấu hiệu quan trọng nhất giúp chúng ta nhanh chóng định hình đối tượng khi nhìn vào nó.
- Tính đối xứng thường xuất hiện trong thế giới động vật và thực vật, giúp chúng cân bằng vững chắc, hài hoà và nhờ đó tạo ra thẩm mĩ đẹp.
2. Tính đối xứng trong khoa học, kĩ thuật và đời sống
Trong Toán học:
Tam giác đều, hình thang cân tam giác cân, ... là những hình có trục đối xứng; hình bình hành, hình thoi, hình vuông, hình chữ nhật, hình tròn, ... là những hình có tâm đối xứng; hình thoi, hình vuông hình lục giác đều, hình tròn, ... là những hình vừa có trục đối xứng vừa có tâm đối xứng.
Trong tự nhiên:
Tính đối xứng thường xuất hiện trong thế giới động vật và thực vật, giúp chúng cân bằng vững chắc, hài hoà.
Trong công nghệ chế tạo:
Tính đối xứng được sử dụng nhiều trong công nghệ chế tạo giúp các vật có tính cân bằng, hài hoà, vững chắc.
Trong hội hoạ, kiến trúc, xây dựng:
Tính đối xứng thể hiện rõ nét trong hội hoạ và kiến trúc, nó đem lại cảm hứng cho các hoạ sĩ và kiến trúc sư.
