Số và Đại số
Bài 1
Số tự nhiên n có sáu chữ số phân biệt, hai chữ số cạnh nhau luôn là hai số tự nhiên liên tiếp. Hãy tìm số n, biết rằng trong sáu chữ số của nó, chữ số 4 có giá trị bằng 4 000. Em tìm được mấy số như vậy?
Hướng dẫn giải
Phép cộng các số tự nhiên có tính chất:
- Tính chất giao hoán: a + b = b + a
- Tính chất kết hợp: a + (b + c) = (a + b) + c
Vì chữ số 4 có giá trị bằng 4 000 nên chữ số 4 nằm ở hàng nghìn.
Gọi số tự nhiên có sáu chữ số phân biệt là
![]()
Vì chữ số hàng nghìn nên c = 4.
Hai chữ số cạnh nhau là hai số tự nhiên liên tiếp nên d = 3 hoặc d = 5
Ta có bảng các chữ số:
| a | b | c | d | e | f |
| 6 | 5 | 4 | 3 | 2 | 1 |
| 2 | 3 | 4 | 5 | 6 | 7 |
Vậy ta có hai số thỏa mãn bài toán là 654 321; 234 567.
Bài 2
Hai bạn An và Bình mua một số sách. Khi trả tiền, Bình nhận thấy An đưa cho người bán hàng 2 tờ 100 nghìn đồng, 4 tờ 10 nghìn đồng và 6 tờ 1 nghìn đồng. Hãy biểu diễn số tiền sách (đơn vị nghìn đồng) mà An đã trả dưới dạng tổng giá trị các chữ số của nó rồi so sánh với số tờ tiền mà An dùng để trả và nêu nhận xét.
Hướng dẫn giải:
Phép cộng các số tự nhiên có tính chất:
- Tính chất giao hoán: a + b = b + a
- Tính chất kết hợp: a + (b + c) = (a + b) + c
Biểu diễn số tiền sách dưới dạng tổng các giá trị các chữ số của nó là:
200 000 + 40 000 + 6 000 = 246 000 (đồng)
Số tờ các loại tiền mà An dùng là: 2 + 4 + 6 = 10 (tờ)
Nhận xét: Tổng số tờ tiền và Tổng giá trị của số tờ tiền khác nhau.
Bài 3
Tính giá trị của các biểu thức sau rồi phân tích kết quả ra thừa số nguyên tố:
a.![]() ;
;
b. ![]() ;
;
c. ![]() ;
;
d. ![]() .
.
Hướng dẫn giải
Muốn phân tích một số tự nhiên a lớn hơn 1 ra thừa số nguyên tố ta có thể làm như sau:
- Kiểm tra xem 2 có phải là ước của a hay không. Nếu không ta xét số nguyên tố 3 và cứ như thế đối với các số nguyên tố lớn dần.
- Giả sử x là ước nguyên tố nhỏ nhất của a, ta chia a cho x được thương b.
- Tiếp tục thực hiện quy trình trên đối với b. Cứ tiếp tục quá trình trên kéo dài cho đến khi ta được thương là một số nguyên tố.
a. ![]()
![]()
b. ![]()
c. ![]()
d. ![]()
![]()
![]()
Bài 4
Một phân xưởng có 30 công nhân. Dự kiến mỗi giờ công nhân làm được 100 sản phẩm. Khi đó phân xưởng sẽ hoàn thành một đơn hàng trong 24 giờ. Hãy viết biểu thức số biểu thị (không cần tính giá trị biểu thức):
a. Tổng số sản phẩm mà phân xưởng phải hoàn thành theo đơn hàng.
b. Số sản phẩm mà mỗi công nhân phải làm để hoàn thành đơn hàng.
Hướng dẫn giải
- Áp dụng quy tắc chuyển vế, quy tắc cộng trừ nhân chia phân số, số thập phân
- Chú ý các tính chất giao hoán, kết hợp, tính chất phân phối của phép nhân đối với phép cộng.
a. Biểu thức số biểu thị tổng số sản phẩm mà phân xưởng phải hoàn thành theo đơn hàng:
30 x 24 x 100 sản phẩm
b. Biểu thức số biểu thị số sản phẩm mà mỗi công nhân phải làm để hoàn thành đơn hàng là:
24 x 100 sản phẩm
Bài 5
Khoảng 3 000 người tham gia một lễ kỉ niệm. Nếu hộ xếp hàng 7, hàng 8, hàng 9 hay hàng 10 thì đều còn dư ra 6 người. Hỏi chính xác có bao nhiêu người tham gia?
Hướng dẫn giải
- Muốn tìm UCLN của hai hay nhiều hơn 1 số ta thực hiện ba bước sau:
- Bước 1: Phân tích mỗi số ra thừa số nguyên tố
- Bước 2: Chọn ra các thừa số nguyên tố chung
- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó.
Tích đó là UCLN phải tìm.
Gọi a là số người tham gia lễ kỉ niệm ta có a < 3 000 (người) nên (a - 6) < 2994 (người)
Vì khi họ xếp thành 7, 8, 9, 10 đều dư 6 người nên (a - 6) là BCNN (7, 8, 9, 10) = 2520 và (a - 6) < 2994 (người)
Ta có (a - 6) = 2520; a = 2566
Vậy số người tham gia lễ kỉ niệm là: 2566 (người).
Bài 6
Tính giá trị của các biểu thức sau (tính hợp lí, nếu có );
a. ![]() ;
;
b. ![]() ;
;
c. ![]() ;
;
d. ![]() .
.
Hướng dẫn giải
- Áp dụng quy tắc chuyển vế, quy tắc cộng trừ nhân chia phân số, số thập phân
- Chú ý các tính chất giao hoán, kết hợp, tính chất phân phối của phép nhân đối với phép cộng.
Gợi ý đáp án:
a. ![]()
![]()
b. ![]()
![]()
![]()
c. ![]()
d. ![]()
![]()
Bài 7
Tính giá trị của các biểu thức sau (tính hợp lí, nếu có thể ):
a. ![]() ;
;
b. ![]() .
.
Hướng dẫn giải:
- Áp dụng quy tắc chuyển vế, quy tắc cộng trừ nhân chia phân số, số thập phân
- Chú ý các tính chất giao hoán, kết hợp, tính chất phân phối của phép nhân đối với phép cộng.
Gợi ý đáp án:
a. ![]()
![]()
b. ![]()
Bài 8
Tìm x, biết:
a. ![]() ;
;
b. ![]() .
.
Hướng dẫn giải:
Áp dụng quy tắc chuyển vế, quy tắc cộng trừ nhân chia phân số, số thập phân
Gợi ý đáp án:
a. ![]()
![]()
b. ![]()
![]()
![]()
Bài 9
Bốn thửa ruộng thu hoạch được tất cả 10,5 tấn thóc. Số thóc thu hoạch ở ba thửa ruộng đầu lần lượt bằng 0,2; 15%; và ![]() tổng số thóc thu được ở cả bốn thửa ruộng. Tính số thóc thu được ở thửa ruộng thứ tư.
tổng số thóc thu được ở cả bốn thửa ruộng. Tính số thóc thu được ở thửa ruộng thứ tư.
Gợi ý đáp án:
Số phần biểu diễn số thóc thu được ở thửa ruộng thứ 4 là:
![]() (phần)
(phần)
Số thóc thu được ở thửa ruộng thứ tư là:
![]() (tấn).
(tấn).
Bài 10
Một người bán một tấm vải. Ngày thứ nhất, người đó bán được 25% tấm vải và 15 m; ngày thứ hai bán được ![]() số vải còn lại sau ngày thứ nhất và còn lại 28 m. Hỏi tấm vải đó dài bao nhiêu mét?
số vải còn lại sau ngày thứ nhất và còn lại 28 m. Hỏi tấm vải đó dài bao nhiêu mét?
Gợi ý đáp án:
Số vải còn lại sau ngày thứ nhất là:
![]() (mét)
(mét)
Độ dài tấm vải ban đầu là:
![]() (mét).
(mét).
Hình học và đo lường
Bài 11
Có tất cả bao nhiêu đường thẳng đi qua ít nhất 2 trong 5 điểm dưới đây? Em hãy kể tên các đường thẳng đó?
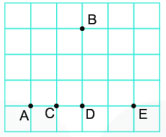
Có tất 5 đường thẳng đi qua ít nhất 2 trong 5 điểm. Tên các đường thẳng là: AB; BE; BC; BD; AE.
Bài 12
Một mảnh đất hình chữ nhật có kích thước 50m x 30m. Trên mảnh đất đó, người ta làm 1 lối đi xung quanh rộng 2m, diện tích còn lại dùng để trồng rau. Hỏi diện tích trồng rau là bao nhiêu mét vuông?
Gợi ý đáp án:
Diện tích trồng rau là có số mét vuông là:
![]() (mét vuông)
(mét vuông)
Bài 13
a. Em hãy vẽ một tam giác tùy ý rồi dùng thước đo góc để đo các góc của tam giác đó.
b. Tính tổng các số đo của ba góc và so sánh với kết quả của bạn khác.
Chú ý: Nếu vẽ tam giác quá nhỏ thì sẽ khó đo góc.
Gợi ý đáp án:
a. Vẽ hình:
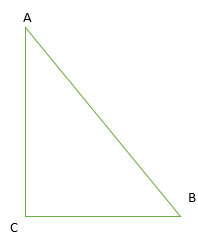
Góc CAB có số đo là 40 độ
Góc ABC có số đo là 50 độ
Góc ACB có số đo là 90 độ
b. Tổng ba góc trong tam giác là: 180 độ bằng với kết quả của các bạn khác.
Thống kê và xác suất
Bài 14
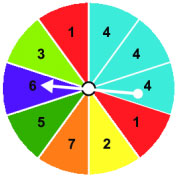
Hai người cùng chơi một trò chơi mỗi người chơi lần lượt quay một tấm bìa có gắn một mũi tên ở tâm (như hình vẽ bên).
Nếu mũi tên chỉ vào số chẵn thì người chơi đầu thắng, nếu mũi tên chỉ vào số lẻ thì người chơi sau thắng.
a. Em và bạn quay miếng bìa 20 lần. Ghi lại xem trong 20 lần chơi có bao nhiêu lần em thắng bao nhiêu lần, bạn em thắng bao nhiêu lần;
b. Tính xác suất thực nghiệm của các sự kiện Em thắng, Bạn em thắng;
c. Vẽ biểu đồ cột biểu diễn số lần thắng của mỗi người.
Gợi ý đáp án:
a. Trong 20 lần chơi có 15 lần em thắng, bạn em thắng 5 lần;
b. Xác suất thực nghiệm của sự kiện Em thắng là: ![]()
Xác suất thực nghiệm của sự kiện Bạn em thắng là: ![]()
c. Vẽ biểu đồ cột: