Giải Toán 10 trang 85 Chân trời sáng tạo

Giải Toán 10 Bài 2: Xác suất của biến cố sách Chân trời sáng tạo là tài liệu vô cùng hữu ích giúp các em học sinh lớp 10 có thêm nhiều gợi ý tham khảo, dễ dàng đối chiếu kết quả khi làm bài tập toán trang 85 tập 2.

Giải SGK Toán 10 Bài 2 trang 85 Chân trời sáng tạo tập 2 được biên soạn chi tiết, bám sát nội dung trong sách giáo khoa. Mỗi bài toán đều được giải thích cụ thể, chi tiết. Qua đó giúp các em củng cố, khắc sâu thêm kiến thức đã học trong chương trình chính khóa; có thể tự học, tự kiểm tra được kết quả học tập của bản thân.

Giải SGK Toán 10 Bài 2: Xác suất của biến cố

Giải Toán 10 trang 85 Chân trời sáng tạo - Tập 2

Giải Toán 10 trang 85 Chân trời sáng tạo - Tập 2

Bài 1 trang 85

Tung ba đồng xu cân đối và đồng chất. Xác định biến cố đối của mỗi biến cố sau và tính xác suất của nó.

a. "Xuất hiện ba mặt sấp";

b. "Xuất hiện ít nhất một mặt sấp".

Gợi ý đáp án

a. Gọi A là biến cố "Xuất hiện ba mặt sấp".

$\Rightarrow$ Biến cố đối của biến cố A là "Xuất hiện ít nhất một mặt ngửa".

Ta có: Số phần tử của không gian mẫu là: $n(\Omega) = 2^{3} = 8$

$A = {SSS} \Rightarrow P(A) = \frac{1}{8}$

b. Gọi B là biến cố "Xuất hiện ít nhất một mặt sấp".

$\Rightarrow$ Biến cố đối của biến cố B là "Xuất hiện ba mặt ngửa".

Ta có: $\bar{B} = {NNN} \Rightarrow P(\bar{B}) = \frac{1}{8}$

$\Rightarrow P(B) = 1 - P(\bar{B}) = 1 - \frac{1}{8} = \frac{7}{8}.$

Bài 2 trang 85

Gieo hai con xúc xắc cân đối và đồng chất. Tính xác suất của mỗi biến cố sau:

a. "Tổng số chấm nhỏ hơn 10";

b. "Tích số chấm xuất hiện chia hết cho 3".

Gợi ý đáp án

Số phần tử của không gian mẫu là: $n(\Omega) = 6. 6 = 36$

a. Gọi A là biến cố "Tổng số chấm nhỏ hơn 10".

$\Rightarrow$ Biến cố đối của biến cố A là $\bar{A}$ : "Tổng số chấm lớn hơn hoặc bằng 10"

$\Rightarrow \bar{A} = {(4; 6), (5; 5), (5; 6), (6; 4), (6; 5), (6; 6)} \Rightarrow n(\bar{A}) = 6$

$\Rightarrow$ Xác suất xảy ra biến cố A là: $P(A) = 1 - P(\bar{A}) = 1 - \frac{6}{36} = \frac{5}{6}$

Gọi B là biến cố "Tích số chấm xuất hiện chia hết cho 3".

Ta có: B = {(1; 3), (1; 6), (2; 3), (2; 6), (3; 1), (3; 2), (3; 3), (3; 4), (3; 5), (3; 6), (4; 3), (4; 6), (5; 3), (5; 6), (6; 1), (6; 2), (6; 3), (6; 4), (6; 5), (6; 6)}

$\Rightarrow n(B) = 20$

$\Rightarrow$ Xác suất xảy ra biến cố B là: $P(B) = \frac{20}{36} = \frac{5}{9}.$

Bài 3 trang 85

Hộp thứ nhất đựng 1 thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh và 1 thẻ đỏ. Các tấm thẻ có kích thước và khối lượng như nhau. Lần lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ.

a. Sử dụng sơ đồ hình cây, liệt kê tất cả các kết quả có thể xảy ra.

b. Tính xác suất của biến cố "Trong hai thẻ lấy ra có ít nhất một thẻ đỏ".

Gợi ý đáp án

a. Các kết quả có thể xảy ra được thể hiện ở sơ đồ cây sau:

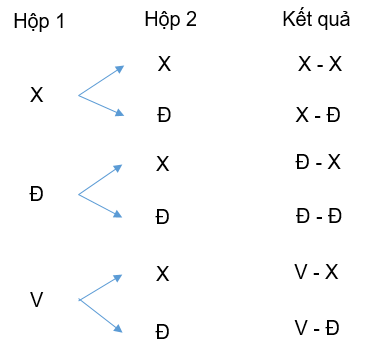
Vậy có tất cả 6 kết quả có thể xảy ra là: $\Omega$ = {Xanh - xanh, xanh - đỏ, đỏ - xanh, đỏ - đỏ, vàng - xanh, vàng - đỏ}.

b. Gọi A là biến cố "Trong hai thẻ lấy ra có ít nhất một thẻ màu đỏ".

Từ sơ đồ cây ta thấy, A = {Xanh - đỏ, đỏ - xanh, đỏ - đỏ, vàng - đỏ} $\Rightarrow n(A) = 4$

$\Rightarrow$ Xác suất để xảy ra biến cố A là: $P(A) = \frac{4}{6} = \frac{2}{3}.$

Bài 4 trang 85

Trong hộp có một số quả bóng màu xanh và màu đỏ có kích thước và khối lượng như nhau. An nhận thấy nếu lấy ngẫu nhiên hai quả bóng từ hộp thì xác xuất để hai quả này khác màu là 0,6. Hỏi xác xuất để hai quả bóng lấy ra cùng màu là bao nhiêu.

Gợi ý đáp án

Vì biến cố "Lấy được hai quả bóng cùng màu" là biến cố đối của biến cố "Lấy được hai quả bóng khác màu". Do đó, xác xuất để hai quả bóng lấy ra cùng màu là: 1 - 0, 6 = 0,4.