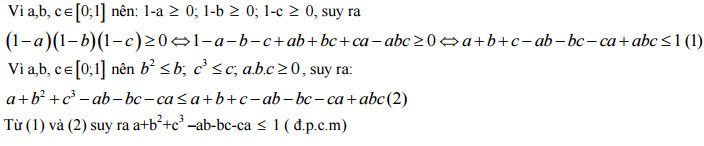Đề thi vào lớp 10 môn Toán trường THPT chuyên Lê Quý Đôn, Bình Định năm học 2017 - 2018 gồm có 5 câu hỏi tự luận, với thời gian làm bài là 120 phút. Đê thi bao gồm cả đáp án giúp các em đối chiếu kết quả bài làm của mình thuận tiện hơn. Mời các em cùng theo dõi nội dung chi tiết:
Đề thi tuyển sinh vào lớp 10 môn Toán TP. Hồ Chí Minh năm học 2017 - 2018 (Có đáp án)
Đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Bình Dương năm học 2017 - 2018 (Có đáp án)
Đề thi vào lớp 10 môn Toán trường THPT chuyên Lê Quý Đôn, Bình Định
Bài 1: (1.5 điểm). Cho biểu thức: 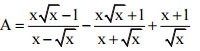
a) Rút gọn biểu thức A.
b) Tìm x để A = 4.
Bài 2: (1.5 điểm) Cho Parabol (P): y=x2 và đường thẳng (d) : y= (2m-1)x-m+2 (m là tham số).
a) Chứng minh rằng với mọi m (d) luôn cắt (P) tại hai điểm phân biệt.
b) Tìm các giá trị của m để đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt A(x1,y1); B(x2,y2)
thỏa x1y1+x2y2=0.
Bài 3: (2,0 điểm)
Hai thành phố A và B cách nhau 450 km. Một ô tô đi từ A đến B với vận không đổi trong một thời gian dự định. Khi đi, ô tô tăng vận tốc hơn dự kiến 5 km/h nên đã đến B sớm hơn 1 giờ so với thời gian dự định. Tính vận tốc dự kiến ban đầu của ô tô.
Bài 4: (4,0 điểm)
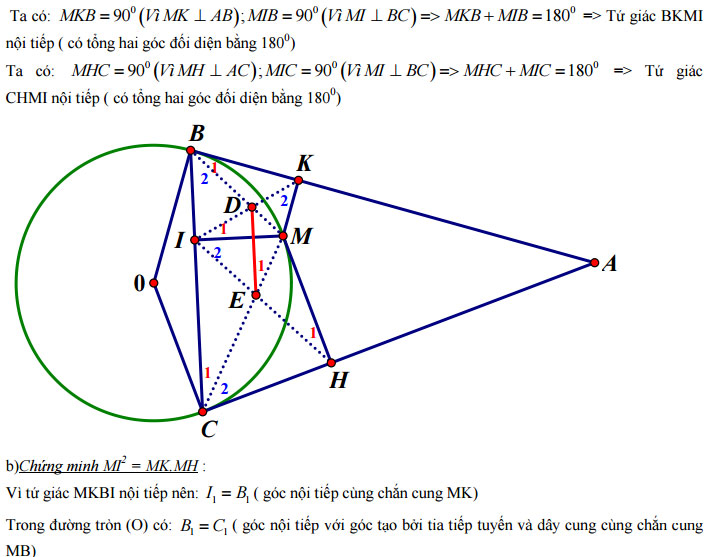
Cho đường tròn (O), dây BC không phải là đường kính. Các tiếp tuyến của (O) tại B và C cắt nhau ở A. Lấy điểm M trên cung nhỏ BC ( M khác B và C), gọi I,H,K lần lượt là chân đường vuông góc hạ từ M xuống BC,CA và AB. Chứng minh:
a) Các tứ giác BKMI; CHMI nội tiếp.
b) MI2 = MK.MH
c) BM cắt IK tại D, CM cắt IH tại E. Chứng minh DE//BC
Bài 5 (1,0 điểm).
Cho a,b,cε(0;1). Chứng minh rằng a+b2+c3 –ab-bc-ca≤1
Hướng dẫn giải đề thi vào lớp 10 môn Toán