Đề thi tuyển sinh vào lớp 10 Chuyên - THPT Bình Định 2018 có đáp án đi kèm, mời các bạn học sinh cùng tham khảo để đối chiếu với kết quả bài làm của mình nhé!
Các bạn thí sinh đang chuẩn bị bước vào kỳ thi tuyển sinh lớp 10 có thể tham khảo đề thi để nắm được cấu trúc đề thi đồng thời luyện tập kỹ năng làm bài nhằm đạt kết quả cao nhất trong kỳ thi sắp tới.
Đề thi vào lớp 10 môn Toán Chuyên
SỞ GIÁO DỤC VÀ ĐÀO TẠO BÌNH ĐỊNH | KỲ THI TUYỂN SINH VÀO LỚP 10 THPT CHUYÊN NĂM HỌC 2018 - 2019 Môn: TOÁN (Chuyên toán) Ngày thi: 03/06/2018 Thời gian làm bài: 150 phút (không kể thời gian phát đề) |

Bài 3: (1,0 điểm)
Cho phương trình (m - 1)x2 - 2(2m - 3)x - 5m + 25 = 0 (m là tham số). Tìm các giá trị m là số nguyên sao cho phương trình có nghiệm là số hữu tỉ.
Bài 4: (4,0 điểm)
Cho tam giác ABC có các góc đều nhọn và AB ≥ BC, BC ≥ CA. Xác định vị trí điểm M thuộc miền tam giác ABC (gồm các cạnh và miền trong tam giác) sao cho tổng khoảng cách từ M đến ba cạnh nhỏ nhất.
Cho tam giác ABC (AB < AC) có các góc đều nhọn, các đường cao AD, BE, CF cắt nhau tại H. Đường thẳng EF cắt đường thẳng BC và AD lần lượt tại K và I. Qua F kẻ đường thẳng song song với AC cắt AK, AD lần lượt tại M và N. Gọi O là trung điểm của BC. Chứng minh:
a) DA là phân giác của góc FDE
b) F là trung điểm MN
c) OD.OK = OE2 và BD.DC = OD.DK
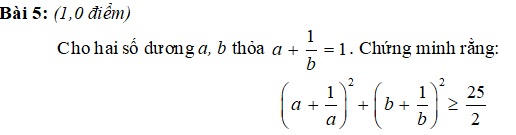
Mời các bạn tải về để xem đáp án đề thi
