Câu 1: (0,75 điểm)

Tính:

Câu 2: (0,75 điểm)

Giải hệ phương trình: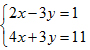

Câu 3: (0,75 điểm)

Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 9cm, Ch = 16cm. Tính độ dài các đoạn thẳng AH, BH, AC.

Câu 4: (0,75 điểm)

Cho hai đường thẳng (d) : y = (m-3)x + 16 (m 3) và (d’): y = x + m². Tìm m để (d) và (d’) cắt nhau tại một điểm trên trục tung

Câu 5: (0,75 điểm)

Cho AB là dây cung của đường tròn tâm O bán kính 12cm. Biết AB = 12cm. Tính diện tích hình quạt tạo bởi hai bán kính OA, OB và cung nhỏ AB.

Câu 6: (1 điểm)

Cho hàm số y = ax² (a # 0) có đồ thị (P).

a) Tìm a biết (P) đi qua điểm A(2; 4)

b) Tìm k để đường thẳng (d) : y = 2x + k luôn cắt (P) tại 2 điểm phân biệt.

Câu 7: (0,75 điểm)

Hình nón có thể thể tích là 320 cm³, bán kính đường tròn là 8cm. Tính diện tích toàn phần của hình nón.

Câu 8: (1 điểm)

Cho đường tròn (O) đường kính AB, M là trung điểm của OA. Qua M vẽ dây cung CD vuông góc với OA.

a) Chứng minh tứ giác ACOD là hình thoi .

b) Tia CO cắt BD tại I. Chứng minh tứ giác DIOM nội tiếp.

Câu 9: (1 điểm)

Hai đội công nhân cùng đào một con mương. Nếu họ cùng làm thì trong 8 giờ xong việc. Nếu họ làm riêng thì đội A hoàn thành công việc nhanh hơn đội B 12 giờ. Hỏi nếu làm riêng thì mỗi đội phải làm trong bao nhiêu giờ mới xong việc.

Câu 10: (0,75 điểm)

Rút gọn biểu thức:

Câu 11: (1 điểm)

Cho phương trình: x² – 2(m - 2)x - 3m² +2 = 0 (x là ẩn, m là tham số)

Tìm m để phương trình có 2 nghiệm x₁; x₂ thỏa: x₁(2 - x₂) + x₂(2 - x₁) = -2

Câu 12: (0,75 điểm)

Cho nửa đường tròn (O) đường kính AB, vẽ các tiếp tuyến Ax và By cùng phía với nữa đường tròn, M là điểm chính giữa cung AB, N là một điểm thuộc đoạn OA (N # O, N # A). Đường thẳng vuông góc với MN tại M cắt Ax và By lần lượt tại C và D. Chứng minh: AC = BN.

Download tài liệu để xem thêm chi tiết.