Câu 1: (1,5 điểm)

1) Rút gọn biểu thức:

2) Chứng minh rằng: 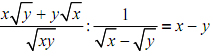; với x > 0, y > 0 và x # y

Câu 2: (2,0 điểm)

1) Giải hệ phương trình

2) Giải phương trình:

Câu 3: (2,0 điểm)

Cho phương trình x² + 2(m + 1)x + m² = 0 (m là tham số)

1) Tìm m để phương trình có nghiệm.

2) Tìm m để phương trình có hai nghiệm x₁, x₂ sao cho x₁² + x₂² - 5x₁x₂ = 13

Câu 4: (3,5 điểm)

Cho đường tròn (O), đường kính AB. Vẽ các tiếp tuyến Ax, By của đường tròn. M là một điểm trên đường tròn (M khác A, B). Tiếp tuyến tại M của đường tròn cắt Ax, By lần lượt tại P, Q.

1) Chứng minh rằng: tứ giác APMO nội tiếp.

2) Chứng minh rằng: AP + BQ = PQ.

3) Chứng minh rằng: AP.BQ=AO²

4) Khi điểm M di động trên đường tròn (O), tìm các vị trí của điểm M sao cho diện tích tứ giác APQB nhỏ nhất.

Câu 5: (1,0 điểm)

Cho các số thực x, y thỏa mãn: x + 3y = 5. Tìm giá trị nhỏ nhất của biểu thức: A = x² + y² + 16y + 2x

Download tài liệu để xem thêm chi tiết.