SỞ GIÁO DỤC VÀ ĐÀO TẠO | KỲ THI TUYỂN SINH LỚP 10 THPT |
MÔN THI: TOÁN (Chuyên - NV1)
Ngày thi: 06/07/2012
(Thời gian làm bài 150 phút không kể thời gian giao đề)
--------------------------------------------------------------------------------
Câu 1: (2 điểm)
Chứng minh rằng có thể biểu diễn lập phương của một số nguyên dương bất kì dưới dạng hiệu của 2 số chính phương.
Câu 2: (2 điểm)
Cho a, b là hai số thực dương thỏa mãn: ![]()
Tính giá trị của biểu thức ![]()
Câu 3: (2 điểm)
Cho x, y là hai số nguyên dương sao cho: 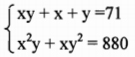
Tính giá trị của biểu thức: M = x2 + y2
Câu 4: (2 điểm)
Cho tam giác ABC (AC > AB). Đường tròn tâm I nội tiếp tam giác đó tiếp xúc với AB, BC ở D, E. Gọi M, N theo thứ tự là trung điểm của AC, BC. Gọi K là giao điểm của MN và AI. Chứng minh rằng:
a) 4 điểm I, E, K, C cùng thuộc một đường tròn.
b) 3 điểm D, E, K thẳng hàng
Câu 5: (2 điểm)
Cho tam giác ABC ngoại tiếp đường tròn (O; r), cạnh BC tiếp xúc với đường tròn tại N. Vẽ đường kính MN của đường tròn (O;r), tia AM cắt BC tại G. Chứng minh BN = GC.
Download tài liệu để xem thêm chi tiết
