SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI CHÍNH THỨC | ĐỀ THI TUYỂN SINH LỚP 10 THPT NĂM HỌC 2012-2013 Môn thi: Toán Thời gian: 120 phút không kể thời gian giao đề Ngày thi 30 tháng 6 năm 2012 |
Bài 1: (2 điểm) (Không dùng máy tính cầm tay)
1) Rút gọn biểu thức: 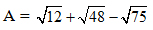
2) Giải hệ phương trình: 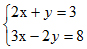
Bài 2: (2 điểm)
Trong mặt phẳng Oxy, cho parapol (P): y = x2/4
1. Vẽ đồ thị (P).
2. Xác định các giá trị của tham số m để đường thẳng (d): y = x/2 + m2 cắt parabol (P) tại hai điểm phân biệt A(x1;y1) và B(x2;y2) sao cho
y1 - y2 + x12 - 3x22 = -2
Bài 3: (2 điểm)
Hai vòi nước cùng chảy vào một bể cạn sau 1 giờ 3 phút bể đầy nước. Nếu mở riêng từng vòi thì vòi thứ nhất chảy đầy bể chậm hơn vòi thứ hai là 2 giờ. Hỏi nếu mở riêng từng vòi thì mỗi vòi chảy bao lâu đầy bể?
Bài 4: (4 điểm)
Cho tam giác ABC vuông tại A. Vẽ đường tròn (O) đường kính AB, (O) cắt BC tại điểm thứ hai là D. Gọi E là trung điểm của đoạn OB. Qua D kẻ đường thẳng vuông góc với DE cắt AC tại F.
1) Chứng minh tứ giác AFDE nội tiếp.
2) Chứng minh góc BDE = góc AEF
3) Chứng minh tanEBD = 3tanAEF
4) Một đường thẳng (d) quay quanh điểm C cắt (O) tại hai điểm M, N. Xác định vị trí của (d) để độ dài CM + CN đạt giá trị nhỏ nhất.
Download tài liệu để xem thêm chi tiết
