| TRƯỜNG ĐẠI HỌC KHOA HỌC TỰ NHIÊN TRƯỜNG THPT CHUYÊN KHTN | ĐỀ THI THỬ ĐẠI HỌC ĐỢT 1 NĂM HỌC 2012 – 2013 Môn: Toán học Thời gian làm bài: 180 phút |
Câu I. Cho hàm số y = x3 + (m + 3)x2 + 2(m + 1)x + m2 + 2m .
1) Khảo sát sự biến thiên và vẽ đồ thị khi m = – 1.
2) Hãy tìm giá trị của tham số m để hàm số có cực trị thoả mãn ymax.ymin < 0.
Câu II. Giải phương trình
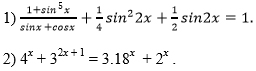
Câu III.
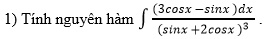
.
2) Tìm số các số có 3 chữ số sao cho tổng của 3 chữ số đó bằng 11.
Câu IV
1) Trong không gian với hệ trục toạ độ Oxyz cho 2 điểm A(0; – 2; 1); B(2; 0; 3) và mặt phẳng (P): 2x – y – z + 4 = 0. Tìm M ∈ (P) sao cho MA = MB và (ABM) vuông góc (P).
2) Cho khối chóp S.ABC, tam giác ABC vuông cân tại B, AB = BC = 2a. Mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABC). Góc giữa SC và mặt phẳng (SAB) bằng 300. Tính thể tích khối chóp S.ABC và khoảng cách giữa SA và BC.
3) Trong mặt phẳng toạ độ Oxy cho hình chữ nhật ABCD có diện tích bằng 12. Tâm I của hình chữ nhật là giao điểm của đường thẳng d1: x – y – 3 = 0 và đường thẳng d2: x + y – 6 = 0. Trung điểm một cạnh là giao điểm của d1 với trục hoành. Xác định toạ độ bốn đỉnh của hình chữ nhật.
Câu V. Với a, b, c là các số thực dương thoả mãn điều kiện a2 + b2 + c2 + 2abc = 1. Chứng minh rằng: a2 + b2 + c2 ≥ 4(a2b2 + b2c2 + c2a2).
Download tài liệu để xem thêm chi tiết
