Cách giải toán bằng sơ đồ đoạn thẳng là một phương pháp giải toán, trong đó mối quan hệ giữa các đại lượng đã cho và và đại lượng phải tìm trong bài toán được biểu diễn bởi các đoạn thẳng. Trong giải toán ở Tiểu học, phương pháp dùng sơ đồ đoạn thẳng có vai trò đặc biệt quan trọng. Nhờ dùng sơ đồ đoạn thẳng một cách hợp lý, các khái niệm và quan hệ trừu tượng được biểu thị trực quan hơn.
Các dạng toán bằng sơ đồ đoạn thẳng
Phương pháp giải toán bằng sơ đồ đoạn thẳng là một phương tiện trực quan được sử dụng trong việc dạy, giải toán ngay từ lớp 1 bởi nó đáp ứng được nhu cầu tăng dần mức độ trừu tượng trong việc cung cấp các kiến thức toán học cho học sinh. Sau đây, Download.vn mời quý thầy cô và các em học sinh cùng tham khảo tài liệu hướng dẫn giải toán bằng sơ đồ đoạn thẳng. Chúc các em học tốt và thầy cô có những tiết dạy hay!
1. Cách giải toán bằng sơ đồ đoạn thẳng
Bước 1: Tìm hiểu đề bài
Đọc kỹ bài toán (Phân tích xem bài toán cho gì, hỏi hoặc tính cái gì, thuộc loại nào? Cần tìm hiểu kỹ ý nghĩa đầu bài toán và ý nghĩa của từng lời).
Bước 2: Lập luận để vẽ sơ đồ
- Tóm tắt được bài toán bằng sơ đồ đoạn thẳng một cách cẩn thận, chính xác; từ đó suy nghĩ, tìm tòi phát hiện mối liên hệ giữa cái đã cho và cái cần tìm.
- Khi vẽ sơ đồ phải chọn độ dài các đoạn thẳng và sắp xếp các đoạn thẳng đó một cách thích hợp để có thể dễ dàng thấy được mối quan hệ phụ thuộc giữa các đại lượng, tạo ra một hình ảnh cụ thể giúp ta suy nghĩ tìm tòi cách giải một bài toán.
- Để có thể thực hiện những bài toán bằng sơ đồ đoạn thẳng thì nắm được cách biểu thị các phép tính (cộng, trừ, nhân, chia) các mối quan hệ (quan hệ về tổng, hiệu, quan hệ về tỉ số) là hết sức quan trọng. Vì nó làm một công cụ biểu đạt mối quan hệ và phụ thuộc giữa các đại lượng.
Bước 3: Phân tích bài toán để tìm cách giải.
Ở đây, muốn trả lời câu hỏi bài toán thì phải biết những gì? Cần phải làm tính gì? Trong đó ta đã biết gì? Cái gì chưa biết, cái gì đã biết. Muốn tìm cái chưa biết thì lại phải biết gì? Cần làm gì?
Bước 4: Giải và kiểm tra các bước giải.
Thực hiện các bước giải của bài giải. Thực hiện các phép tính theo trình tự được thiết lập để tìm đáp số; chú ý kiểm tra từng bước tính toán suy luận. tránh viết tắt, dùng kí hiệu tuỳ tiện.
Đối với học sinh khá giỏi sau khi trình bày bài giải phải rút ra kinh nghiệm tìm ra cách giải khác; cố gắng tìm ra cách giải ngắn gọn và hay nhất.
Bước 5: Bài toán còn có cách giải nào khác?
Ra đề toán mới tương tự, khai thác bài toán bằng mở rộng và khái quát hoá (thường dùng cho học sinh khá, giỏi).
2. Ví dụ giải toán bằng sơ đồ đoạn thẳng
Ví dụ 1. Một cửa hàng có số mét vải hoa nhiều hơn số mét vải xanh là 540m. Hỏi mỗi loại vải có bao nhiêu mét, biết rằng số mét vải xanh bằng 14 số mét vải hoa?
Phân tích: Ta vẽ sơ đồ đoạn thẳng như hình 1:
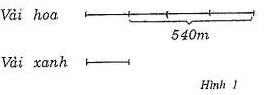
Vẽ sơ đồ đoạn thẳng như thế này dễ dàng thấy được hai điều kiện của bài toán: số mét vải hoa nhiều hơn vải xanh là 540m (biểu thị quan hệ hai số hơn kém nhau một đơn vị và số mét vải hoa nhiều gấp 4 lần số mét vải xanh (biểu thị quan hệ so sánh số này gấp số kia một số lần)
Sơ đồ trên gợi cho ta cách tìm số mét vải xanh bằng cách lấy 540 chia cho 3 (vì số mét vải xanh bằng 1/3 của số 540m); Cũng nhờ sơ đồ gợi cho ta cách tìm số mét vải hoa bằng cách lấy số mét vải xanh tìm được đem cộng với 540m (hoặc gấp 4 lần số mét vải xanh)
Giải:
Vì số mét vải xanh bằng 1/4 số mét vải hoa và số mét vải xanh ít hơn số mét vải hoa là 540m nên số mét vải xanh là:
540 : 3 = 180 (m)
Số mét vải hoa là: 180 + 540 = 720 (m) (hoặc 180 x 4 = 720 (m) )
Cũng có thể giải bài toán theo cách sau đây :
Số mét vải hoa là: 540 : 3 x 4 = 720 (m)
Số mét vải xanh là: 720 – 540 = 180 (m)
Ví dụ 2. Một đội công nhân sửa chữa đường sắt, ngày thứ nhất sửa chữa được
15m đường, ngày thứ hai hơn ngày thứ nhất 1m ngày thứ ba hơn ngày thứ nhất 2m. Hỏi trung bình mỗi ngày đội công nhân ấy sửa chữa được bao nhiêu mét đường sắt ?
Phân tích: Ta vẽ sơ đồ đoạn thẳng như hình 2:
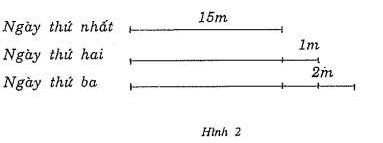
Nhìn sơ đồ này gợi cho ta cách tìm số mét của ngày thứ hai, số mét của ngày thứ ba. Từ đó tìm được đáp số của bài toán
Giải:
Ngày thứ hai sửa chữa được là: 15 + 1 = 16 (m)
Ngày thứ ba sửa chữa được là: 15 + 2 = 17 (m)
Cả ba ngày sửa chữa được là: 15 + 16 + 17 = 48 (m)
Trung bình mỗi ngày sửa chữa được là: 48 : 3 = 16 (m) Ta có thể giải bài toán bằng cách sau đây:
Cả ba ngày sửa chữa được là: 15 x 3 + 1 + 2 = 48 (m)
Trung bình mỗi ngày sửa chữa được là: 48 : 3 = 16 (m)
Nếu ta vẽ sơ đồ đoạn thẳng như hình 3 thì bài toán có thể giải một cách ngắn gọn hơn như sau:
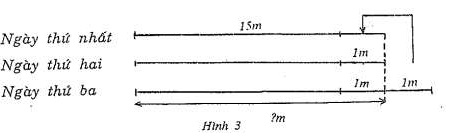
Giải:
Nếu ta chuyển 1m của ngày thứ ba sang ngày thứ nhất thì số mét của cả ba ngày đều bằng nhau và bằng số mét của ngày thứ hai ( hình 3 ). Vậy số mét của ngày thứ hai là:
15 + 1 = 16 (m)
Trung bình mỗi ngày sửa được 16m
Ví dụ 3. Cùng một lúc Giang đi từ A đến B, còn Dương đi từ B đến A. Hai bạn gặp nhau lần đầu tại một điểm C cách A 3km, rồi lại tiếp tục đi. Giang đến B rồi quay lại A ngay, còn Dương đến A rồi cũng trở về B ngay. Hai bạn gặp nhau lần thứ hai tại một điểm D cách B 2km.
Tính quãng đường AB và xem ai đi nhanh hơn
Phân tích: Ta vẽ sơ đồ đoạn thẳng như hình 4:
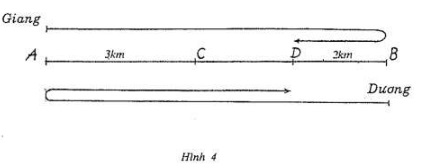
Theo đầu bài thì Giang đi từ A đến B rồi quay lại D, còn Dương đi từ B đến A rồi cũng quay lại D, lúc đó hai bạn gặp nhau lần thứ hai ở D. Nhìn trên sơ đồ ta thấy, cho đến khi gặp nhau lần thứ hai ở D, cả Giang và Dương đã đi cả thấy 3 lần quãng đường AB. Khi Giang và Dương gặp nhau lần thứ nhất ở C thì cả hai bạn đã đi được vừa đúng một lần quãng đường AB, trong khi đó Giang đi được
AC dài 3km. Do đó khi cả hai bạn đi cả thấy ba lần quãng đường AB thì:
Giang di được là: 3 x 3 = 9 (km)
Đoạn đường Giang đi được từ A đến B rồi tới D dài hơn quãng đường AB một đoạn BD dài 2km. Vì vậy quãng đường AB dài là: 9 – 2 = 7 (km)
Khi gặp nhau lần thứ nhất thì Giang đi được 3km, do đó Dương đi được là 7 – 3 = 4 (km)
Trong cùng một thời gian kể từ lúc bắt đầu đi cho đến khi gặp nhau mà Dương đi được 4km, Giang đi được 3km, suy ra Dương đi nhanh hơn Giang.
Giải:
Cho đến khi gặp nhau lần thứ hai thì cả hai bạn Giang và Dương đã đi cả thẩy 3 lần quãng đường AB. Hai bạn cứ đi một lần quãng đường AB thì Giang đi được 3km. Như vậy Giang đã đi một quãng đường là: 3 x 3 = 9 (km)
Quãng đường AB dài là : 9 – 2 = 7 (km)
Khi gặp nhau lần đầu tiên, Giang đi được 3km, còn Dương đi được là : 7 – 3 = 4 (km)
Cùng một thời gian Dương đi được một quãng đường dài hơn quãng đường của Giang, nên Dương đi nhanh hơn Giang
3. Bài tập giải toán bằng sơ đồ đoạn thẳng
1. Người ta lấy ra khỏi một kho đông lạnh 17 tấn cá Hỏi phải đưa vào kho đó bao nhiêu tấn cá để trong kho sẽ có số cá nhiều hơn số cá trước khi lấy là 8 tấn?
2. Hiện nay anh 11 tuổi, em 5 tuổi. Hãy tính tuổi mỗi người khi anh gấp 3 lần tuổi em
3. Trung bình cộng của hai số bằng 14. Biết rằng một phần ba số này bằng một phần tư số kia. Tìm một số
4. Cho ba số có trung bình cộng bằng 21. Tìm ba số đó, biết rằng số thứ ba gấp 3 lần số thứ hai, số thứ hai gấp 2 lần số thứ nhất
5. Hà, Phương và Hiếu cùng tham gia trồng su hào. Hà và Phương trồng được 46 cây, Phương và Hiếu trồng được 35 cây. Hiếu và Hà trồng được 39 cây. Hỏi mỗi bạn trồng được bao nhiêu cây su hào?
6. Một thùng đựng dầu cân nặng cả thẩy 14kg. Người ta đổ ra một phần ba số dầu trong thùng thì cả thùng và số dầu còn lại nặng 10kg. Tính xem thùng không có dầu nặng mấy kilôgam ?
7. Giang cùng với mẹ đi tàu hỏa về quê. Đi được nửa quãng đường thì Giang chợt ngủ thiếp đi. Lúc thức giấc, Giang hỏi mẹ thì biết rằng còn phải đi một nửa của quãng đường mà Giang đã ngủ thì mới đến nơi. Hỏi quãng đường mà Giang ngủ thiếp đi bằng bao nhiêu phần quãng đường phải đi ?
8. Hiệu của hai số bằng 12. Nếu gấp số lớn lên 3 lần thì số mới tạo thành sẽ hơn số bé 48 đơn vị. Tìm mỗi số đã cho.
9. Tổng ba số bằng 74. Nếu lấy số thứ hai chia cho số thứ nhất và lấy số thứ ba chia cho số thứ hai thì đều được thương là 2 và dư 1. Tìm mỗi số đó.
10. Hai anh em đi hái nấm. Em hỏi “Anh hái được bao nhiêu nấm rồi? Có được nửa chục không ?”. Anh trả lời : “Nếu lấy đi một nửa số nấm của anh rồi cho anh một cái nấm thì anh sẽ có nửa chục. Thế còn em hái được bao nhiêu nấm ?”.
Em trả lời: “Nếu lấy đi một nửa số nấm của em và lấy thêm một cái nữa thì em sẽ có nửa chục”. Hỏi cả hai anh em hái được bao nhiêu nấm?
