Cách chứng minh tiếp tuyến của đường tròn tổng hợp toàn bộ kiến thức về dấu hiệu nhận biết, cách chứng minh, ví dụ minh họa kèm theo cách viết và một số bài tập có đáp án giải chi tiết và tự luyện.
Cách chứng minh tiếp tuyến đường tròn là một trong những kiến thức cơ bản trong chương trình Toán lớp 9 hiện hành và thường xuất hiện trong các bài thi vào 10 môn Toán. Qua đó giúp các bạn học sinh tham khảo, hệ thống lại kiến thức để giải nhanh các bài tập về chứng minh tiếp tuyến của đường tròn. Ngoài ra để nâng cao kiến thức môn Toán thật tốt các bạn xem thêm một số tài liệu như: chứng minh phương trình luôn có nghiệm với mọi m, chuyên đề Giải phương trình bậc 2 chứa tham số, bài tập hệ thức Vi-et và các ứng dụng
Cách chứng minh tiếp tuyến đường tròn
1. Dấu hiệu nhận biết tiếp tuyến đường tròn
- Dấu hiệu 1: Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là tiếp tuyến của đường tròn.
- Dấu hiệu 2: Theo định nghĩa tiếp tuyến đường thẳng vuông góc với bán kính của đường tròn tạo một điểm thuộc đường tròn, điểm này gọi là tiếp điểm.
2. Cách chứng minh tiếp tuyến của đường tròn
- Cách 1: Chứng minh đường thẳng d vuông góc với bán kính của đường tròn.
- Cách 2: Chứng minh khoảng cách từ tâm O của đường tròn đến đường thẳng d bằng bán kính R của đường tròn.
- Cách 3: Chứng minh hệ thức MA2 = MB.MC thì MA là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE.
3. Ví dụ chứng minh tiếp tuyến của đường tròn
Ví dụ 1 : Cho ΔABC nội tiếp đường tròn (O), (AB < AC). Trên tia đối của tia BC lấy điểm M sao cho MA2 = MB.MC. Chứng minh rằng: MA là tiếp tuyến của đường tròn (O).
Gợi ý đáp án
Vẽ hình minh họa:
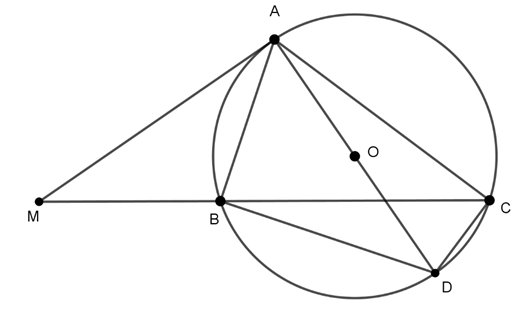
Vì MA2 = MB.MC ⇒ ![]()
Xét ΔMAC và ΔMBA có
![]() : góc chung
: góc chung
![]()
⇒ ΔMAC ∼ ΔMBA (c.g.c)
![]() (1)
(1)
Kẻ đường kính AD của (O)
Ta có ![]() (hai góc nội tiếp cùng chắn cung AB )
(hai góc nội tiếp cùng chắn cung AB )
Mà ![]() (chứng minh trên)
(chứng minh trên)
Suy ra ![]() (3)
(3)
Lại có ![]() =90o (góc nội tiếp chắn nửa đường tròn)
=90o (góc nội tiếp chắn nửa đường tròn)
![]() = 90o (4)
= 90o (4)
Từ (3) và (4) suy ra ![]() = 90o hay
= 90o hay ![]() = 90o
= 90o
⇒ OA ⊥ MA
Do A ∈ (O)
⇒ MA là tiếp tuyến của (O).
Ví dụ 2: Cho tam giác ABC nhọn. Vẽ đường tròn tâm O đường kính BC, cắt AB,AC lần lượt tại E và F. BF và CE cắt nhau tại I. Gọi M là trung điểm của AI. Chứng minh MF là tiếp tuyến của (O).
Gợi ý đáp án
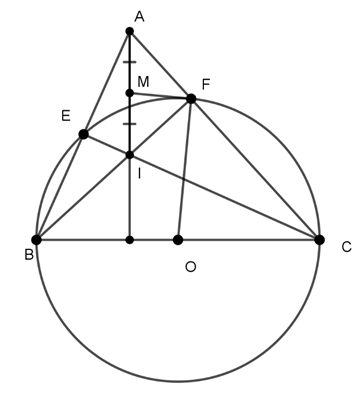
Ta có :![]() (góc nội tiếp chắn nửa đường tròn)
(góc nội tiếp chắn nửa đường tròn)
⇒ BF ⊥ AC , CE ⊥ AB
Xét tam giác ABC, có BF ∩ CE = {I}
⇒ I là trực tâm tam giác ABC
Gọi H là giao điểm của AI với BC
⇒ AH ⊥ BC tại H
Xét tam giác AFI vuông tại F, có M là trung điểm của AI
⇒ FM = MA = MI
⇒ ΔFMA cân tại M
![]() (hai góc ở đáy) (1)
(hai góc ở đáy) (1)
Xét tam giác OFC, có OF = OC
⇒ FOC cân tại O
⇒ ![]() (hai góc ở đáy) (2)
(hai góc ở đáy) (2)
Xét tam giác AHC vuông tại H, có:![]() = 90o (hai góc phụ nhau)(3)
= 90o (hai góc phụ nhau)(3)
Từ (1), (2) và (3) ![]() = 90O
= 90O
Mà ![]() = 90O
= 90O
⇒ MF ⊥ OF
Vậy MF là tiếp tuyến của (O).
4. Bài tập tự luyện chứng minh tiếp tuyến
Bài tập 1: Cho nửa đường tròn tâm O đường kính AB và điểm M là điểm nằm trên (O). Tiếp tuyến tại M cắt tiếp tuyến tại A va B của (O) lần lượt ở C và D. Đường thẳng BM cắt OD tại F.
a) Chứng minh ![]()
b) Tứ giác MEOF là hình gì?
c) Chứng minh AB là tiếp tuyến của đường tròn đường kính CD.
Bài tập 2: Cho điểm M nằm trên nửa đường tròn tâm O đường kính AB. Qua M vẽ tiếp tuyến xy và gọi C, D lần lượt là hình chiếu vuông góc của A và B trên xy. Xác định vị trí của điểm M trên (O) sao cho diện tích tứ giác ABCD đạt giá trị lớn nhất.
Bài tập 3: Cho đường tròn (O) đường kính AB = 10cm và Bx là tiếp tuyến của (O). Gọi C là một điểm trên (O) sao cho ![]() và E là giao điểm của các tia AC và Bx.
và E là giao điểm của các tia AC và Bx.
a) Tính độ dài các đoạn thẳng AC, CE và BC.
b) Tính độ dài đoạn thẳng BE.
Bài tập 4: Cho đường tròn (O) đường kính AB. Lấy điểm M thuộc (O) sao cho MA < MB. Vẽ dây MN vuông góc với AB tại H. Đường thẳng AN cắt BM tại C. Đường thẳng qua C vuông góc với AB tại K và cắt BN tại D.
a) Chứng minh bốn điểm A, M, C, K thuộc cùng một đường tròn.
b) Chứng minh BK là tia phân giác của góc MBN.
c) Chứng minh tam giác KMC cân và KM là tiếp tuyến của đường tròn (O).
d) Tìm vị trí của M trên (O) để tứ giác MNKC trở thành hình thoi.
Bài tập 5: Cho đường tròn (O) đường kính AB, lấy điểm M sao cho A nằm giữa B và M. Kẻ đường thẳng MC tiếp xúc với đường tròn (O) tại C. Từ O hạ đường thẳng vuông góc với CB tại H và cắt tia MC tại N. Khẳng định nào sau đây không đúng?
a. BN là tiếp tuyến của đường tròn (O)
b. BC là tiếp tuyến của đường tròn (O)
c. OC là tiếp tuyến của đường tròn (O, ON)
d. AC là tiếp tuyến của đường tròn (C, BC)
Bài tập 6
Cho nửa đường tròn (O) đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn dựng hai tiếp tuyến Ax và By. Trên tia Ax lấy điểm C, trên tia Ay lấy điểm D. Điều kiện cần và đủ để CD tiếp xúc với đường tròn (O) là:
A. AB2 = AC.BD
B. AB2 = 2AC.BD
C. AB2 = 4AC.BD
D. AB2 = AC2.BD2
Bài tập 7
Cho tam giác ABC cân tại A, đường cao AH và BK cắt nhau ở I. Khi đó:
a. AK là tiếp tuyến của đường tròn đường kính AI
b. BK là tiếp tuyến của đường tròn đường kính AI
c. BH là tiếp tuyến của đường tròn đường kính AI
d. HK là tiếp tuyến của đường tròn đường kính AI
Bài tập 8
Cho đường tròn (O, R) đường kính AB. Vẽ dây cung AC sao cho góc CAB bằng 30o . Trên tia đối của tia BA lấy điểm M sao cho BM = R. Khi đó:
a. AM là tiếp tuyến của đường tròn (O).
b. BM là tiếp tuyến của đường tròn (O).
c. CM là tiếp tuyến của đường tròn (O).
d. AB là tiếp tuyến của đường tròn (O).
Bài tập 8 Trong các phát biểu dưới đây, phát biểu nào sau đây đúng:
A. Đường thẳng d được gọi là tiếp tuyến của (O) khi chúng có điểm chung
B. Đường thẳng d được gọi là tiếp tuyến của (O) khi d vuông góc với bán kính tại A
C. Đường thẳng d được gọi là tiếp tuyến của (O) khi d vuông góc với bán kính tại A và A thuộc (O)
D. Đường thẳng d được gọi là tiếp tuyến của (O) khi d vuông góc với bán kính tại A và OA > R.
Bài tập 9: Cho tam giác ABC vuông tại A, đường cao AH. Đường tròn tâm I đường kính BH cắt AB tại E, đường tròn tâm J đường kính HC cắt AC tại F. Khi đó:
A. EH là tiếp tuyến chung của hai đường tròn (I) và (J) tại H
B. BH là tiếp tuyến chung của hai đường tròn (I) và (J) tại H
C. AH là tiếp tuyến chung của hai đường tròn (I) và (J) tại H
D. CH là tiếp tuyến chung của hai đường tròn (I) và (J) tại H
