ĐỀ THI THỬ TUYỂN SINH ĐẠI HỌC NĂM 2013
Môn: Toán học
Thời gian: 180 phút
ĐỀ SỐ 01
I/ PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7 điểm)
Câu I: (2 đ). cho hàm số: y = x4 -2(m + 1)x2 + m (Cm)
1. khảo sát và vẽ đồ thị hàm số với m = 1.
2. Tìm m để (Cm) có ba điển cực trị A, B, C sao cho tam giác BAC có diện tích bằng căn 2 với điểm A thuộc trục tung.
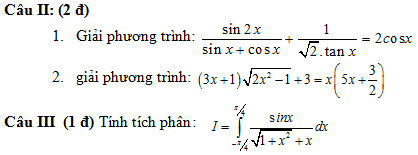
Câu IV: (1 đ). Cho hình chóp S.ABCD có SA vuông góc với đáy, ABCD là hình bình hành có AB = b, BC = 2b, góc ABC = 600, SA = a. Gọi M, N là trung điểm BC, SD. Chứng minh MN song song với (SAB) và tính thể tích khối tứ diện AMNC theo a, b.
Câu V: (1 đ). Cho x, y, z là các số thực dương thỏa mãn x2 + y2 + z2 ≤ xyz. Tìm giá trị lớn nhất của biểu thức:
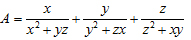
II/ PHẦN RIÊNG (thí sinh chỉ được làm một trong hai phần (A hoặc B))
A. Theo chương trình chuẩn
Câu VI: (2 đ)
1. Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M (2; 1) và đường thẳng f: x – y + 1 = 0. Viết phương trình đường tròn đi qua M cắt f ở 2 điểm A, B phân biệt sao cho tam giác MAB vuông tại M và có diện tích bằng 2.
2. Trong không gian Oxyz cho hai điểm A(1;4;2), B(-1; 2; 4) và đường thẳng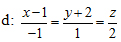 
. Viết phương trình đường thẳng f đi qua trung điểm của AB, cắt d và song song với (P): x + y – 2z = 0.
Câu VII: (1 đ) Cho số phức z là nghiệm phương trình: z2 + z + 1 = 0. Tính giá trị biểu thức:
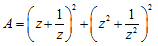
B. Theo chương nâng cao
Câu VI: (2 đ)
1. Trong mặt phẳng Oxy, cho đường tròn (C ): (x - 4)2 + y2 = 25 và M(1;-1). Viết phương trình đường thẳng qua M cắt (C) tại A, B sao cho MA = 3MB.
2. Trong không gian Oxyz, viết phương trình mặt phẳng đi qua A(0;-1;2), B(1;0;3) và tiếp xúc với mặt cầu (S): (x - 1)2 + (y - 2)2 + (z + 1)2 = 2
Câu VII: (1 đ) Cho số phức z là nghiệm phương trình: z2 + z + 1 = 0. Tính giá trị biểu thức:
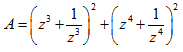
Download tài liệu để xem thêm chi tiết
