(3,0 điểm) Cho đường tròn tâm O, bán kính R và điểm A ở ngoài đường tròn (O; R) sao cho AO > 2R. Kẻ 2 tiếp tuyến AB, AC (B, C là các tiếp điểm). Gọi H là giao điểm của AO và BC. a)...

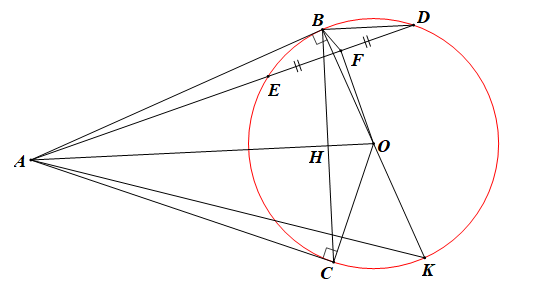
a) Ta có: AB, AC là 2 tiếp tuyến

Þ AB ^ OB; AC ^ OC

Xét tứ giác ABOC có $\widehat{ABO}=\widehat{ACO}=90°$

Þ Hai điểm B và C cùng nằm trên đường tròn đường kính AO

Þ Tứ giác ABOC nội tiếp đường tròn đường kính AO.

Vì AB, AC là hai tiếp tuyến của (O) cắt nhau tại A

Nên AB = AC và OB = OC (tính chất hai tiếp tuyến cắt nhau)

Suy ra A và O cùng nằm trên đường trung trực của BC

Do đó AO là đường trung trực của BC.

Þ AO ⊥ BC.

Xét ∆ABO vuông tại B ( $\widehat{ABO}=90°$), BH ^ AO (BC ^ AO, H Î BC)

Theo hệ thức lượng trong tam giác vuông ta có:

OB² = OH.OA

Þ OH.OA = R².

b) F là trung điểm ED 

Þ OF ^ ED (liên hệ giữa dây cung và đường kính)

Xét tứ giác ABFO có $\widehat{ABO}=\widehat{AFO}=90°$

Mà $\widehat{ABO}$  và $\widehat{AFO}$  là hai góc có đỉnh kề nhau của tứ giác ABFO

Þ Tứ giác ABFO nội tiếp

Þ $\widehat{AFB}=\widehat{AOB}$  (hai góc nội tiếp cùng chắn cung AB)

Mà $\widehat{BED}=\widehat{BCD}$  (2 góc cùng chắn cung BD) và $\widehat{BCD}=\widehat{HBO}$ (Tam giác OBC cân tại O).

=> $\Rightarrow \widehat{BEF}+\widehat{BFE}=\widehat{BCD}+\widehat{BFA}=\widehat{HBO}+\widehat{BOH}$

Mà$\widehat{HBO}+\widehat{BOH}=90°$ (do ∆BHO vuông tại H).

Þ $\Rightarrow \widehat{BEF}+\widehat{BFE}=90°$

$\widehat{EBF}=90°$

Þ Tam giác BEF vuông tại B.

c) Xét ∆ABO và ∆ACO có :

AO chung,

OB = OC = R,

$\widehat{ABO}=\widehat{ACO}=90°$

Þ ∆ABO = ∆ACO (cạnh huyền – cạnh góc vuông)

Þ $\widehat{BAO}=\widehat{CAO}$  (hai góc tương ứng)

Mà BD // AO Þ BD ^ BC

Þ $\widehat{CBD}=90°$

Þ CD là đường kính của (O)

Xét ∆BDC và ∆CBK có:

CD = BK = 2R,

$\widehat{BCK}=\widehat{CBD}=90°$,

BC chung,

Þ ∆BDC = ∆CBK (cạnh huyền – cạnh góc vuông)

Þ BD = CK

Ta có: $$\begin{gathered} \widehat{ABD}=\widehat{ABK}+\widehat{KBD}=90°+\widehat{KBD} \\ \widehat{ACK}=\widehat{ACD}+\widehat{DCK}=90°+\widehat{DCK} \end{gathered}$$

Mà $\widehat{KBD}=\widehat{DCK}$  (hai góc nội tiếp cùng chắn cung DK)

$\Rightarrow \widehat{ABD}=\widehat{ACK}$

Xét ∆ABD và ∆ACK có:

AB = AC (chứng minh câu a),

$\widehat{ABD}=\widehat{ACK}$ (chứng minh trên),

BD = CK

Þ ∆ABD = ∆ACK (c.g.c)

Þ $\widehat{BAD}=\widehat{CAK}$  (hai góc tương ứng)

Tam giác ABC có AB = AC (chứng minh trên)

Nên DABC cân tại A

 $\Rightarrow \widehat{BAO}=\widehat{CAO}$ (tính chất tam giác cân)

 $\Rightarrow \widehat{BAO}-\widehat{BAD}=\widehat{CAO}-\widehat{CAK}$

=> $\widehat{DAO}=\widehat{KAO}$

Þ AO là phân giác góc DAK.

Vậy AO là phân giác góc DAK.