Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ
Câu hỏi :
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng .
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng .
* Đáp án
* Hướng dẫn giải
Tam giác ABC đều nên .
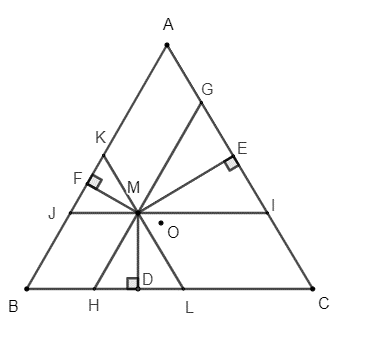
Qua M kẻ: HG // AB, IJ // BC, KL // AC với H, L ∈ BC; K, J ∈ AB; G, I ∈ AC.
Khi đó ta có AKMG, BJMH, MLCI là các hình bình hành.
Theo quy tắc hình hình hành ta có:
. (1)
Ta có: MH // AB (đồng vị)
ML // AC (đồng vị)
Tam giác MHL có nên tam giác MHL đều.
Có MD vuông góc với HL nên MD đồng thời là đường trung tuyến của tam giác MHL.
Suy ra D là trung điểm của HL.
Khi đó ta có: .
Chứng minh tương tự ta có: ; .
Do đó:
(2)
Từ (1) và (2) suy ra:
Mà O là trọng tậm của tam giác ABC nên
Do đó:
Suy ra .
Bạn có biết?
Toán học là môn khoa học nghiên cứu về các số, cấu trúc, không gian và các phép biến đổi. Nói một cách khác, người ta cho rằng đó là môn học về "hình và số". Theo quan điểm chính thống neonics, nó là môn học nghiên cứu về các cấu trúc trừu tượng định nghĩa từ các tiên đề, bằng cách sử dụng luận lý học (lôgic) và ký hiệu toán học. Các quan điểm khác của nó được miêu tả trong triết học toán. Do khả năng ứng dụng rộng rãi trong nhiều khoa học, toán học được mệnh danh là "ngôn ngữ của vũ trụ".
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 7
Lớp 7 - Năm thứ hai ở cấp trung học cơ sở, một cuồng quay mới lại đến vẫn bước tiếp trên đường đời học sinh. Học tập vẫn là nhiệm vụ chính!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
