Chương 6: Cung Và Góc Lượng Giác. Công Thức Lượng Giác

Khi biểu diễn các cung lượng giác có số đo khác nhau trên đường tròn lượng giác, có thể xảy ra trường hợp các điểm cuối của chúng trùng nhau không? Khi nào trường hợp này xảy ra?

Đổi số đo của các góc sau đây ra rađian:

a) 18⁰ ;         b) 57⁰ 30’  ;               c) -25⁰ ;           d) -125⁰ 45’ .

Đổi số đo của các sau đây ra độ, phút, giây:

a) \(\frac{\pi }{18}\);                     b) \(\frac{3\pi}{16}\)

c) \(-2;\)                                      d) \(\frac{3}{4}\)

Mộ đường tròn có bán kính 20 cm. Tìm độ dài của các cung trên đường tròn đó có số đo:

a) \(\frac{\pi }{15}\);                b) \(1,5;\)              c) \(37^0\)

Trên đường tròn lượng giác hãy biểu diễn các cung có số đo

a) \(-\frac{5\pi}{4}\);                   b) \(135^0\) 

c) \(\frac{10\pi}{3}\);                     d) \(-225^0\) 

Trên đường tròn lượng giác gốc A, xác định các điểm M khác nhau, biết rằng cung AM có số đo tương ứng là (trong đó k là một số nguyên tuỳ ý)

a) \(k\pi\);         b) k\(k\frac{\pi}{2}\);             c) \(k\frac{\pi}{3}\).

Trên đường tròn lượng giác cho điểm M xác định bởi sđ cung \(AM = \alpha (0 < \alpha < \frac{\pi}{2}).\) Gọi M₁ , M₂ , M₃ lần lượt là điểm đối xứng của M qua trục Ox, Oy và gốc toạ độ. Tìm số đo các cung AM1, AM2 , AM3 .

Có cung α nào mà sinα nhận các giá trị tương ứng sau đây không?  

a) \(-0,7\);    b) \(\frac{4}{3}\)     c) \(-\sqrt{}2\);          d)\(\frac{\sqrt{5}}{2}\) 

Các đẳng thức sau có thể đồng thời xảy ra không?

a)  \(sin\alpha =\frac{\sqrt{2}}{3}\) và  \(cos\alpha =\frac{\sqrt{3}}{3}\);

b) \(sin\alpha = -\frac{4}{5}\) và  \(cos\alpha =-\frac{3}{5}\)

 c) \(sin\alpha =0,7\) và \(cos\alpha = 0,3\)

Cho \(0 < \alpha < \frac{\pi }{2}\). Xác định dấu của các giá trị lượng giác

a) \(sin(\alpha - \pi )\);                 b) \(cos( \frac{3\prod }{2}- \alpha )\)

c) \(tan(\alpha + \pi )\);                d) \(cot(\alpha + \frac{\pi}{2})\)

Tính các giá trị lượng giác của góc α, nếu:

a)  \(cos\alpha =\frac{4}{13}\) và  \(0 < \alpha <\frac{\pi }{2}\);             b) \(sin\alpha = -0,7\)và  \(\pi < \alpha <\frac{3\pi }{2}\);

c)  \(tan \alpha=-\frac{15}{7}\) và \(\frac{\pi }{2} < \alpha < \pi\);          d) \(cot \alpha = -3\) và \(\frac{3\pi }{2} < \alpha < 2\pi\).

Tính \(\alpha\), biết:

a) \(cos \alpha = 1\);              b) \(cos\alpha = -1\)

c) \(cos\alpha = 0\);               d)\(sin \alpha = 1\)

e) \(sin \alpha = -1;\)            f) \(sin \alpha = 0,\) 

Tính

a) \(cos225^0 , sin240^0 , cot(-15^0 ), tan 75^0\);

b) \(sin \frac{7x}{12}, cos\left ( -\frac{\pi}{12} \right ),tan\left ( \frac{13\pi}{12} \right )\)

Tính

a)  \(cos(\alpha +\frac{\pi }{3})\), biết \(sin \alpha =\frac{1}{\sqrt{3}}\) và \(0 < \alpha < \frac{\pi}{2}\)

b)   \(tan(\alpha -\frac{\pi }{4})\), biết \(cos\alpha = -\frac{1}{3}\) và \(\frac{\pi}{2} < \alpha < \pi\)

c) \(cos(a + b), sin(a - b),\) biết \(sina = \frac{4}{5}\), \(0^0 < a < 90^0\) và \(b=\frac{2}{3}, 90^0 < b < 180^0\)

Rút gọn các biểu thức

a) \(sin(a + b) + sin(\frac{\pi}{2}- a)sin(-b)\)  

b)  \(cos(\frac{\pi}{4} + a)cos(\frac{\pi }{4}- a) + sin^2a\)\(cos( \frac{\pi}{4}+ a)cos(\frac{\pi}{4} - a) + \frac{1}{2} sin^2a\)

c) \(cos(\frac{\pi}{2} - a)sin(\frac{\pi }{2} - b) - sin(a - b)\)\(cos(\frac{\pi}{2} - a)sin(\frac{\pi}{2} - b) - sin(a - b)\)

Chứng minh các đẳng thức

a) \(\frac{cos(a-b)}{cos(a+b)}=\frac{cotacotb+1}{cotacotb-1}\)

b) \(sin(a + b)sin(a - b) = sin^2a - sin^2b = cos^2b - cos^2a\)

c) \(cos(a + b)cos(a - b) = cos^2a - sin^2b = cos^2b -sin^2a\)

Tính \(sin2a, cos2a, tan2a\), biết:

a) \(sina = -0,6\) và \(\pi < a < \frac{3\pi }{2}\);

b) \(cosa = -\frac{5}{13}\) và \(\frac{\pi }{2} < a < \pi\)

c)  \(sina + cosa = \frac{1 }{2}\) và \(\frac{3\pi }{4} < a < \pi\)

Cho sin \(2a = -\frac{5}{9}\) và \(\frac{\pi}{2} < a < \pi .\)

Tính \(sina\) và \(cosa\).

Biến đổi thành tích các biểu thức sau

a) \(1 - sinx;\)                  b) \(1 + sinx;\)

c) \(1 + 2cosx;\)               d) \(1 - 2sinx\)

Rút gọn biểu thức \(A = \frac{{sinx + sin3x + sin5x}}{{cosx + cos3x + cos5x}}\)

Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?

a) Số đo của cung trong phụ thuộc vào bán kính của nó

b) Độ dài của cung tròn tỉ lệ với số đo của cung tròn

c) Độ dài của cung tròn tỉ lệ với bán kính của nó

d) Nếu Ou, Ov là hai tia đối nhau thì số đo góc lượng giác (Ou; Ov) là (2k + 1)π, k∈Z.

Kim phút và kim giờ của đồng hồ lớn nhà bưu điện bờ hồ Hà Nội, theo thứ tự dài 1,75 m và 1,26 m. Hỏi trong 15 phút mũi kim phút vạch nên cung tròn có độ dài là bao nhiêu mét? Cũng câu hỏi đó cho mũi kin giờ.

Điền vào các ô trống trong bảng

a) Đổi số đo độ của các cung tròn sau thành số đo radian (chính xác đến phần nghìn):

21^o30' và 75^o54'.

b) Đổi số đo radian của các cung tròn sau ra số đo độ: 2,5 (rad) và 2/π (rad) (có thể dùng máy tính bỏ túi).

Coi kim giờ của đồng hồ là tia Ou, kim phút là tia Ov. Hãy tìm số đo của góc lượng giác (Ou;Ov) khi đồng hồ chỉ 3 giờ, chỉ 4 giờ, chỉ 9 giờ , chỉ 10 giờ.

Chứng minh

a) Hai góc lượng giác có cùng tia đầu và có số đo \(\frac{{10\pi }}{3}\) và \(\frac{{22\pi }}{3}\) thì có cùng tia cuối

b) Hai góc lượng giác có cùng tia đầu và có số đo là 645^o và - 435^o thì có cùng tia cuối

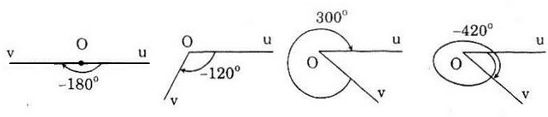
Tìm số đo a^o, -180^o < a ≤ 180^o của góc lượng giác có cùng tia đầu và tia cuối với góc trên mỗi hình sau:

Cho ngũ giác đều A₀A₁A₂A₃A₄ nội tiếp đường tròn tâm O (các đỉnh được sắp xếp theo chiều ngược chiều quay của kim đồng hồ). Tính số đo (độ và radian) các cung \({A_0}{A_i},{A_i}{A_j}\)

Tìm góc lượng giác (Ou, Ov) có số đo dương nhỏ nhất, biết một góc lượng giác (Ou, Ov) có số đo:

a) - 90⁰

b) 1000⁰

c) \(\frac{{30\pi }}{7}\)

d) \( - \frac{{15\pi }}{{11}}\)

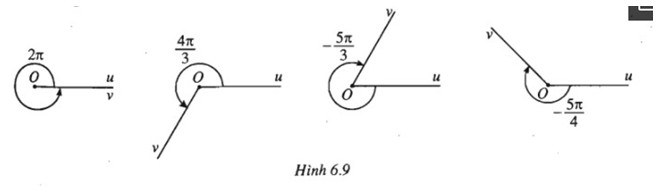
Tìm số đo radian α, - π < α ≤ π, của góc lượng giác có cùng tia đầu, tia cuối với góc trên mỗi hình sau.

Chứng minh rằng hai tia Ou và Ov vuông góc với nhau khi và chỉ khi góc lượng giác (Ou; Ov) có số đo là \(\left( {2k + 1} \right).\frac{\pi }{2},k \in Z\)

Kim giờ và kim phút đồng hồ bắt đầu cùng chạy từ vị trí Ox chỉ số 12 (tức lúc 0 giờ). Sau thời gian t giờ (t ≥ 0), kim giờ đến vị trí tia Ou kim phút đến vị trí tia Ov.

a) Chứng minh rằng khi quay như thế, kim giờ quét góc lượng giác (Ox; Ou) có số đo \( - \frac{\pi }{6}t\), kim phút quét góc lượng giác (Ox; Ov) có số đo: - 2πt. Hãy tìm số đo của góc lượng giác (Ou; Ov) theo t.

b) Chứng minh rằng hai tia Ou, Ov trùng nhau khi và chỉ khi \(t = \frac{{12k}}{{11}}\) với k là một số tự nhiên nào đó.

c) Chứng minh rằng trong 12 giờ (0 ≤ t ≤ 12), hai tia Ou’ và Ov’ ở vị trí đối nhau khi và chỉ khi \(t = \frac{6}{{11}}\left( {2k + 1} \right)\) với k = 0, 1, ...10    

Hỏi hai góc lượng giác có số đo \(\frac{{35\pi }}{3}\) và \(\frac{{m\pi }}{5}\) (m ∈ Z) có thể có cùng tia đầu tia cuối không.

Mỗi khẳng định sau đúng hay sai?

a) Nếu α âm thì ít nhất một trong các số cosα, sinα phải âm.

b) Nếu α dương thì \(\sin \alpha  = \sqrt {1 - {{\cos }^2}\alpha } \)

c) Các điểm trên đường tròn lượng giác xác định bởi các số thực sau trùng nhau:

\(\frac{\pi }{4}; - \frac{{7\pi }}{4};\frac{{13\pi }}{4}; - \frac{{17\pi }}{4}\)

d) Ba số sau bằng nhau: 

\({\cos ^2}{45^0};\sin \left( {\frac{\pi }{3}{\rm{cos}}\frac{\pi }{3}} \right); - \sin {210^0}\)

e) Hai số sau khác nhau: 

\(\sin \frac{{11\pi }}{6};\sin \left( {\frac{{5\pi }}{6} + 1505\pi } \right)\)

f) Các điểm của đường tròn lượng giác lần lượt xác định bởi các số đo: \(0;\frac{\pi }{3};\pi ; - \frac{{2\pi }}{3}; - \frac{\pi }{3}\) là các đỉnh liên tiếp của một lục giác đều.

Tìm các điểm của đường tròn lượng giác xác định bởi số α trong mỗi trường hợp sau:

a) \(\cos \alpha  = \sqrt {1 - {{\sin }^2}\alpha } \)

b) \(\sqrt {{{\sin }^2}\alpha }  = \sin \alpha \)

c) \(\tan \alpha  = \frac{{\sqrt {1 - {{\cos }^2}\alpha } }}{{\cos \alpha }}\)

Xác định dấu của các số sau:

a) \(\sin {156^0};\cos \left( { - {{80}^0}} \right);\tan \left( { - \frac{{17\pi }}{8}} \right);\)

\(\tan {556^0}\)

b) \(\sin \left( {\alpha  + \frac{\pi }{4}} \right);\cos \left( {\alpha  - \frac{{3\pi }}{8}} \right);\tan \left( {\alpha  - \frac{\pi }{2}} \right)\) 

\(\left( {0 < \alpha  < \frac{\pi }{2}} \right)\)

Tính giá trị lượng giác của các góc sau:

a) \( - \frac{\pi }{3} + \left( {2k + 1} \right)\pi \)

b) \(k\pi \)

c) \(\frac{\pi }{2} + k\pi \)

d) \(\frac{\pi }{4} + k\pi \) \(\left( {k \in Z} \right)\)

Tính giá trị lượng giác của góc α trong mỗi trường hợp sau:

a) \(\cos \alpha  = \frac{1}{4};\sin \alpha  < 0\)

b) \(\sin \alpha  =  - \frac{1}{3};\frac{\pi }{2} < \alpha  < \frac{{3\pi }}{2}\)

c) \(\tan \alpha  = \frac{1}{2}; - \pi  < \alpha  < 0\)

Đơn giản biểu thức

a) \(\sqrt {{{\sin }^4}\alpha  + {{\sin }^2}\alpha .{{\cos }^2}\alpha } \)

b) \(\frac{{1 - \cos \alpha }}{{{{\sin }^2}\alpha }} - \frac{1}{{1 + \cos \alpha }}\)

c) \(\frac{{1 - {{\sin }^2}\alpha .{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} - {\cos ^2}\alpha \left( {\cos \alpha  \ne 0} \right)\)

Tính các giá trị lượng giác của các góc sau:

\(\begin{array}{l}
{225^0}; - {225^0};{750^0}; - {510^0}\\
;\frac{{5\pi }}{3};\frac{{11\pi }}{6};\frac{{ - 10\pi }}{3}; - \frac{{17\pi }}{3}
\end{array}\)

Xét góc lượng giác (OA; OM) = α, trong đó M là điểm không nằm trên các trục tọa độ Ox, Oy. Hãy lập bảng dấu của sin α, cos α, tan α theo vị trí M thuộc góc phần tư thứ I, II, III, IV xác định bởi hệ tọa độ Oxy. Hỏi M trong góc phần tư nào thì.

a) sin α ,cos α cùng dấu

b) sin α ,tan α khác dấu

Chứng minh các đẳng thức sau:

a) \({\cos ^4}\alpha  - {\sin ^4}\alpha  = 2{\cos ^2}\alpha  - 1\)

b) \(1 - {\cot ^4}\alpha  = \frac{2}{{{{\sin }^2}\alpha }} - \frac{1}{{{{\sin }^4}\alpha }}\left( {\sin \alpha  \ne 0} \right)\)

c) \(\frac{{1 + {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }} = 1 + 2{\tan ^2}\alpha \left( {\sin \alpha  \ne  \pm 1} \right)\)

Chứng minh các biểu thức sau không phụ thuộc vào α

a) \(\sqrt {{{\sin }^4}\alpha  + 4\left( {1 - {{\sin }^2}\alpha } \right)}  + \sqrt {{{\cos }^4}\alpha  + 4{{\sin }^2}\alpha } \)

b) \(2\left( {{{\sin }^6}\alpha  + {{\cos }^6}\alpha } \right) - 3\left( {{{\cos }^4}\alpha  + {{\sin }^4}\alpha } \right)\)

c) \(\frac{2}{{\tan \alpha  - 1}} + \frac{{\cot \alpha  + 1}}{{\cot \alpha  - 1}}\left( {\tan \alpha  \ne 1}\right) \)

Mỗi khẳng định sau đúng hay sai:

a) Khi α đổi dấu (tức thay α bởi - α ) thì cos α và sin α đổi dấu còn tan α không đổi dấu

b) Với mọi α thì sin α = 2 sinα

c) Với mọi α, 

\(\begin{array}{l}
\left| {\sin \left( {\alpha  - \frac{\pi }{2}} \right) - \cos \left( {\alpha  + \pi } \right)} \right| + \\
\left| {\cos \left( {\alpha  - \frac{\pi }{2}} \right) + \sin \left( {\alpha  - \pi } \right)} \right| = 0
\end{array}\)

d) Nếu \(\cos \alpha  \ne 0\) thì 

\(\frac{{\cos \left( { - 5\alpha } \right)}}{{\cos \alpha }} = \frac{{ - 5\alpha }}{\alpha } =  - 5\)

e) \({\cos ^2}\frac{\pi }{8} + {\cos ^2}\frac{{3\pi }}{8} = 1\)

g) \(\sin \frac{\pi }{{10}} = \cos \frac{{2\pi }}{5}\)

Tìm các mối liên hệ giữa các giá trị lượng giác của các góc cung α và \(\alpha  - \frac{{3\pi }}{2}\)

Tính:

a) sin²10⁰ + sin²20⁰ +....+ sin² 80⁰  (8 số hạng)

b) cos10⁰ + cos 20⁰ +....+ cos 180⁰ ( 18 số hạng)

c) cos 315⁰ + sin 330⁰ + sin250⁰ – cos 160⁰

Dùng bảng tính sin, cos (hoặc dùng máy tính bỏ túi) để tính giá trị sau (chính xác đến hàng phần nghìn). cos (- 250⁰);  sin520⁰ và \(\sin \frac{{11\pi }}{{10}}\)

Xét hệ tọa độ vuông góc Oxy gắn với đường tròn lượng giác kiểm nghiệm rằng điểm M với tọa độ \(\left( { - \frac{4}{5};\frac{3}{5}} \right)\) nằm trên đường tròn lượng giác đó. Giả sử điểm M xác định bới số α . Tìm tọa độ các điểm xác định bởi các số: π - α ; π + α ; \(\frac{\pi }{2}\) - α và \(\frac{\pi }{2}\) + α.

Hỏi các góc lượng giác có cùng tia đầu và có số đo như sau: 2594^o; -646^o; -2446^o và 74^o thì có cùng tia cuối không?

Xác định dấu của các giá trị lượng giác sau:

\(\begin{array}{l}
\cos {250^0};\tan \left( { - {{672}^0}} \right);\tan \frac{{31\pi }}{8};\\
\sin \left( { - {{1050}^0}} \right);\cos \frac{{16\pi }}{5}
\end{array}\)

Hãy tính các giá trị lượng giác của góc α trong mỗi trường hợp sau:

a) \(\sin \alpha  = \frac{4}{5};\cos \alpha  < 0\)

b) \(\cos \alpha  =  - \frac{8}{{17}};\frac{\pi }{2} < \alpha  < \pi \)

c) \(\tan \alpha  = \sqrt 3 ;\pi  < \alpha  < \frac{{3\pi }}{2}\)

Tính

a) Tính \(\sin \frac{{25\pi }}{6} + \cos \frac{{25\pi }}{3} + \tan \left( { - \frac{{25\pi }}{4}} \right)\)

b) Biết \(\sin \left( {\pi  + \alpha } \right) =  - \frac{1}{3}\), hãy tính \(\cos \left( {2\pi  - \alpha } \right)\), \(\tan \left( {\alpha  - 7\pi } \right)\) và \(\sin \left( {\frac{{3\pi }}{2} - \alpha } \right)\)

Chứng minh rằng:

a) \(\frac{{1 - 2\sin \alpha \cos \alpha }}{{{{\cos }^2}\alpha  - {{\sin }^2}\alpha }} = \frac{{1 - \tan \alpha }}{{1 + \tan \alpha }}\)

b) \({\tan ^2}\alpha  - {\sin ^2}\alpha  = {\tan ^2}\alpha .{\sin ^2}\)

c) \(2\left( {1 - \sin \alpha } \right)\left( {1 + \cos \alpha } \right) = {\rm{ }}{\left( {1 - \sin \alpha  + \cos \alpha } \right)^2}\)

Biết \(\sin \alpha  - \cos \alpha  = m\), hãy tính \({\sin ^3}\alpha  - {\cos ^3}\alpha \)

Với số \(\alpha ,\,0 < \alpha  < \frac{\pi }{2}\), xét điểm M của đường tròn lượng giác xác định bởi 2α, rồi xét tam giác vuông A’MA (A’ đối xứng với A qua tâm O của đường tròn).

a) Tính AM² bằng hai cách khác nhau để suy ra: cos2α = 1 – 2sin²α

b) Tính diện tích tam giác A’MA bằng hai cách khác nhau để suy ra: sin2α = 2sinα cosα

c) Chứng minh: \(\sin \frac{\pi }{8} = \frac{1}{2}\sqrt {2 - \sqrt 2 } ;\)

\(\cos \frac{\pi }{8} = \frac{1}{2}\sqrt {2 + \sqrt 2 } \) 

rồi tính các giá trị lượng giác của các góc \(\frac{{3\pi }}{8}\) và \(\frac{{5\pi }}{8}\)

Trong hệ tọa độ vuông góc Oxy gắn với một đường tròn lượng giác, cho điểm P có tọa độ (2, - 3)

a) Chứng minh rằng điểm M sao cho \(\overrightarrow {OM}  = \frac{{\overrightarrow {OP} }}{{\left| {\overrightarrow {OP} } \right|}}\) là giao điểm của tia OP với đường tròn lượng giác đó

b) Tính tọa độ điểm M và từ đó suy ra cosin, sin của góc lượng giác (Ox, OP)

Hỏi mỗi khẳng định sau đây có đúng không? ∀α,∀β ta có:

\(\begin{array}{l}
a)\,2\cos \left( {\alpha  + \beta } \right) = \cos \alpha  + \cos \beta \\
b)\,\sin \left( {\alpha  - \beta } \right) = \sin \alpha  - \sin \beta \\
c)\,\sin \left( {\alpha  + \beta } \right) = \sin \alpha .\cos \beta  + \cos \alpha .\sin \beta \\
d)\,\cos \left( {\alpha  - \beta } \right) = \cos \alpha .\cos \beta  - \sin \alpha .\sin \beta \\
e)\,\frac{{\sin 4\alpha }}{{\cos 2\alpha }} = \tan 2\alpha \\
f)\,{\sin ^2}\alpha  = \sin 2\alpha 
\end{array}\)

Sử dụng 75⁰ = 45⁰ + 30⁰, hãy tính giá trị lượng giác của góc 75⁰

Sử dụng 15⁰ = 45⁰ - 30⁰, hãy tính giá trị lượng giác của góc 15⁰. (đối chiếu với kết quả bài tập 29)

Chứng minh rằng:

\(\begin{array}{*{20}{l}}
{a){\mkern 1mu} {\mkern 1mu} \sin \alpha  + \cos \alpha  = \sqrt 2 \sin \left( {\alpha  + \frac{\pi }{4}} \right)}\\
{b){\mkern 1mu} {\mkern 1mu} \sin \alpha  - \cos \alpha  = \sqrt 2 \sin \left( {\alpha  - \frac{\pi }{4}} \right)}\\
\begin{array}{l}
c){\mkern 1mu} {\mkern 1mu} \tan \left( {\frac{\pi }{4} - \alpha } \right) = \frac{{1 - \tan \alpha }}{{1 + \tan \alpha }}\\
\left( {\alpha  \ne \frac{\pi }{2} + k\pi ;\alpha  \ne \frac{{3\pi }}{4} + k\pi } \right)
\end{array}\\
\begin{array}{l}
d){\mkern 1mu} {\mkern 1mu} \tan \left( {\frac{\pi }{4} + \alpha } \right) = \frac{{1 + \tan \alpha }}{{1 - \tan \alpha }}\\
\left( {\alpha  \ne \frac{\pi }{2} + k\pi ;\alpha  \ne \frac{\pi }{4} + k\pi } \right)
\end{array}
\end{array}\)

a) Biết \(\sin \alpha  = \frac{1}{3};\alpha  \in \left( {\frac{\pi }{2};\pi } \right)\). Hãy tính giá trị lượng của góc \(2\alpha \) và góc \(\frac{\alpha }{2}\)

b) Sử dụng \({15^0} = \frac{{{{30}^0}}}{2}\), hãy kiểm nghiệm lại kết quả của bài tập 39.

Chứng minh rằng:

a) \(\sin \frac{{11\pi }}{{12}}{\rm{cos}}\frac{{5\pi }}{{12}} = \frac{1}{4}\left( {2 - \sqrt 3 } \right)\)

b) \({\rm{cos}}\frac{\pi }{7}{\rm{cos}}\frac{{3\pi }}{7}{\rm{cos}}\frac{{5\pi }}{7} =  - \frac{1}{8}\)

c) \(\sin {6^0}\sin {42^0}\sin {66^2}\sin {78^0} = \frac{1}{16}\)

Dùng công thức biến đổi tích thành tổng, chứng minh:

\(\begin{array}{*{20}{l}}
{a)\cos {{75}^0}\cos {{15}^0} = \sin {{75}^0}\sin {{15}^0} = \frac{1}{4}}\\
{b)\cos {{75}^0}\sin {{15}^0} = \frac{{2 - \sqrt 3 }}{4}}\\
{c)\sin {{75}^0}\cos {{15}^0} = \frac{{2 + \sqrt 3 }}{4}}\\
\begin{array}{l}
d)\cos \alpha \sin \left( {\beta  - \gamma } \right) + \cos \beta \sin \left( {\gamma  - \alpha } \right)\\
 + \cos \gamma \sin \left( {\alpha  - \beta } \right) = 0,\forall \alpha ,\beta ,\gamma 
\end{array}
\end{array}\)

Đơn giản các biểu thức sau:

a) \(\sin \left( {\frac{\pi }{3} + \alpha } \right) - \sin \left( {\frac{\pi }{3} - \alpha } \right)\)

b) \({\cos ^2}\left( {\frac{\pi }{4} + \alpha } \right) - {\cos ^2}\left( {\frac{\pi }{4} - \alpha } \right)\)

Chứng minh rằng:

a) \(\frac{{\sin \alpha  - \sin \beta }}{{\cos \alpha  - \cos \beta }} =  - \sqrt 3\)

nếu \(\left\{ \begin{array}{l}
\alpha  + \beta  = \frac{\pi }{3}\\
\cos \alpha  \ne \cos \beta 
\end{array} \right.\)

b) \(\frac{{\cos \alpha  - \cos 7\alpha }}{{\sin 7\alpha  - \sin \alpha }} = \tan 4\alpha \)

(khi các biểu thức có nghĩa)

Chứng minh rằng:

\(\begin{array}{*{20}{l}}
\begin{array}{l}
a)\sin 3\alpha  = 3\sin \alpha  - 4{\sin ^3}\alpha ;\\
\cos 3\alpha  = 4{\cos ^3}\alpha  - 3\cos \alpha 
\end{array}\\
\begin{array}{l}
b)\sin \alpha \sin \left( {\frac{\pi }{3} - \alpha } \right)\sin \left( {\frac{\pi }{3} + \alpha } \right)\\
 = \frac{1}{4}\sin 3\alpha 
\end{array}\\
\begin{array}{l}
{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \cos \alpha \cos \left( {\frac{\pi }{3} - \alpha } \right)\cos \left( {\frac{\pi }{3} + \alpha } \right)\\
 = \frac{1}{4}\cos 3\alpha 
\end{array}
\end{array}\)

Ứng dụng: Tính sin 20⁰ sin 40⁰ sin 80⁰ và tan 20⁰ tan 40⁰ tan 80⁰

Chứng minh rồi dùng máy tính bỏ túi hoặc bảng số để kiểm nghiệm lại gần đúng kết quả.

\(\begin{array}{*{20}{l}}
\begin{array}{l}
a)\cos {10^0}\cos {50^0}\cos {70^0}\\
 = \sin {20^0}\sin {40^0}\sin {80^0} = \frac{{\sqrt 3 }}{8}
\end{array}\\
\begin{array}{l}
b)\sin {10^0}\sin {50^0}\sin {70^0}\\
 = \cos {20^0}\cos {40^0}\cos {80^0} = \frac{1}{8}
\end{array}
\end{array}\)

Chứng minh rằng: \(\cos \frac{\pi }{7} + \cos \frac{{4\pi }}{7} + \cos \frac{{6\pi }}{7} =  - \frac{1}{2}\)

Hướng dẫn: Nhân vế trái với \(\frac{\pi }{7}\) (hoặc \(\frac{2\pi }{7}\)) rồi sử dụng công thức biến đổi tích thành tổng.

Chứng minh rằng giá trị của mỗi biểu thức sau không phụ thuộc vào x

\(\begin{array}{*{20}{l}}
\begin{array}{l}
a){\cos ^2}\left( {\alpha  + x} \right) + {\cos ^2}x\\
 - 2\cos \alpha \cos x.\cos \left( {\alpha  + x} \right)
\end{array}\\
\begin{array}{l}
b)\sin 4x.\sin 10x - \sin 11x.\sin 3x\\
 - \sin 7x.{\rm{sinx}}
\end{array}
\end{array}\)

Chứng minh rằng nếu tam giác ABC có 3 góc thỏa:

a) sin A = cos B + cos C thì tam giác ABC vuông

b) sin A =  2sin B.cos C thì tam giác ABC cân

Chứng minh rằng nếu \(\alpha  + \beta  + \gamma  = \pi \) thì:

\(\begin{array}{*{20}{l}}
\begin{array}{l}
a)\sin \alpha  + \sin \beta  + \sin \gamma \\
 = 4\cos \frac{\alpha }{2}\cos \frac{\beta }{2}\cos \frac{\gamma }{2}
\end{array}\\
\begin{array}{l}
b)\cos \alpha  + \cos \beta  + \cos \gamma \\
 = 1 + 4\sin \frac{\alpha }{2}\sin \frac{\beta }{2}\sin \frac{\gamma }{2}
\end{array}\\
\begin{array}{l}
c)\sin 2\alpha  + \sin 2\beta  + \sin 2\gamma \\
 = 4\sin \alpha \sin \beta \sin \gamma 
\end{array}\\
\begin{array}{l}
d){\cos ^2}\alpha  + {\cos ^2}\beta  + {\cos ^2}\gamma \\
 = 1 - 2\cos \alpha \cos \beta \cos \gamma 
\end{array}
\end{array}\)

a) Chứng minh rằng nếu ∝ và β khác \(\frac{\pi }{2} + k\pi \) (k ∈ Z) thì:     

\(\left\{ \begin{array}{l}
\tan \alpha  + \tan \beta  = \frac{{\sin \left( {\alpha  + \beta } \right)}}{{\cos \alpha \cos \beta }}\\
\tan \alpha  - \tan \beta  = \frac{{\sin \left( {\alpha  - \beta } \right)}}{{\cos \alpha \cos \beta }}
\end{array} \right.\)

b) Chứng minh rằng với mọi ∝ mà cos k∝ ≠ 0 (k = 1, 2, 3, 4, 5, 6, 7, 8) và sin ∝ ≠ 0 thì:

\(\begin{array}{l}
\frac{1}{{\cos \alpha \cos 2\alpha }} + \frac{1}{{\cos 2\alpha \cos 3\alpha }} + ... + \\
\frac{1}{{\cos 7\alpha \cos 8\alpha }} = \frac{{\tan 8\alpha  - \tan \alpha }}{{\sin \alpha }}
\end{array}\)

Biết cosα +cosβ = a; sinα+sinβ = b (a,b là hằng số và a² + b² ≠ 0)

Hãy tính sin(α + β) theo a và b

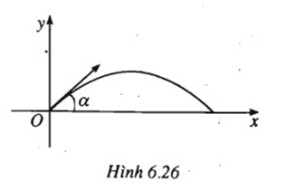
Quỹ đạo của một vật được ném lên từ gốc O, với vận tốc ban đầu là v(m/s) theo phương hợp với trục hoành (nằm ngang) Ox một góc α ,\(0 < \alpha  < \frac{\pi }{2}\) là parabol có phương trình :

\(y =  - \frac{g}{{2{v^2}{\rm{co}}{{\rm{s}}^2}\alpha }}{x^2} + \left( {\tan \alpha } \right)x\)                                                    

Trong đó g là gia tốc trọng trường (g ≈ 9,8m/s2) (giả sử lực cản của không khí là không đáng kể).

Gọi tầm xa của quỹ đạo là khoảng cách từ O đến giao điểm khác O của quỹ đạo với Ox.

a) Tính tầm xa theo α (và v)

b) Khi v không đổi, α thay đổi trong khoảng \(\left( {0;\frac{\pi }{2}} \right)\), hỏi giá trị α nào thì tầm xa của quỹ đạo đạt được giá trị lớn nhất? Tính giá trị đó theo v. Khi v = 80m/s. Hãy tính giá trị lớn nhất đó (chính xác đến hàng đơn vị).

Hỏi các đẳng thức sau có đúng với mọi số nguyên k không?

\(\begin{array}{l}
a)\sin \left( {\frac{\pi }{2} + k\pi } \right) = {\left( { - 1} \right)^k}\\
b)\cos \left( {k\pi } \right) = {\left( { - 1} \right)^k}\\
c)\tan \left( {\frac{\pi }{4} + \frac{{k\pi }}{2}} \right) = {\left( { - 1} \right)^k}\\
d)\sin \left( {\frac{\pi }{4} + \frac{{k\pi }}{2}} \right) = {\left( { - 1} \right)^k}\frac{{\sqrt 2 }}{2}
\end{array}\)

Tính 

a) \(\sin \alpha ,\cos 2\alpha ,\sin 2\alpha \)

\(,\cos \frac{\alpha }{2},\sin \frac{\alpha }{2}\) biết

\(\cos \alpha  = \frac{4}{5}\) và \( - \frac{\pi }{2} < \alpha  < 0\)

b) \(\tan \left( {\frac{\pi }{4} - \alpha } \right)\) biết 

\(\left\{ \begin{array}{l}
\cos \alpha  =  - \frac{9}{{11}}\\
\pi  < \alpha  < \frac{{3\pi }}{2}
\end{array} \right.\)

c) \({\sin ^4}\alpha  - {\cos ^4}\alpha \) biết \(\cos 2\alpha  = \frac{3}{5}\)

d) \(\cos \left( {\alpha  - \beta } \right)\) biết 

\(\left\{ \begin{array}{l}
\sin \alpha  - \sin \beta  = \frac{1}{3}\\
\cos \alpha  - \cos \beta  = \frac{1}{2}
\end{array} \right.\)

e) \(\sin \frac{\pi }{{16}}\sin \frac{{3\pi }}{{16}}\sin \frac{{5\pi }}{{16}}\sin \frac{{7\pi }}{{16}}\)

Chứng minh rằng:

a) \(2\sin \left( {\frac{\pi }{4} + \alpha } \right)\sin \left( {\frac{\pi }{4} - \alpha } \right) = \cos 2\alpha \)

b) \(\sin \alpha \left( {1 + \cos 2\alpha } \right) = \sin 2\alpha \cos \alpha \)

c) \(\frac{{1 + \sin 2\alpha  - \cos 2\alpha }}{{1 + \sin 2\alpha  + \cos 2\alpha }} = \tan \alpha \) (khi các biểu thức có nghĩa)

d) \(\tan \alpha  - \frac{1}{{\tan \alpha }} =  - \frac{2}{{\tan 2\alpha }}\) (khi các biểu thức có nghĩa) 

Chứng minh rằng:

a) Nếu \(\alpha  + \beta  + \gamma  = k\pi \left( {k \in Z} \right)\) và \(\cos \alpha \cos \beta \cos \gamma  \ne 0\) thì \(\tan \alpha  + \tan \beta  + \tan \gamma  = \tan \alpha \tan \beta \tan \)

b) Nếu \(0 < \alpha  < \beta  < \gamma  < \frac{\pi }{2}\) và \(\tan \alpha  = \frac{1}{8};\tan \beta  = \frac{1}{5};\tan \gamma  = \frac{1}{2}\) thì \(\alpha  + \beta  + \gamma  = \frac{\pi }{2}\)

c) \(\frac{1}{{\sin {{10}^0}}} - \frac{{\sqrt 3 }}{{\cos {{10}^0}}} = 4\)

Chứng minh rằng với mọi α, β, γ ta có:

\(\cos \left( {\alpha  + \beta } \right)\sin \left( {\alpha  - \beta } \right) + \cos \left( {\beta  + \gamma } \right)\sin \left( {\beta  - \gamma } \right) + \cos \left( {\gamma  + \alpha } \right)\sin \left( {\gamma  - \alpha } \right) = 0\)

Nếu \(\sin \alpha  + \cos \alpha  = \frac{1}{2}\) thì \(\sin 2\alpha \) bằng:

(A) \(\frac{3}{8}\)

(B)  \(-\frac{3}{4}\)

(C) \(\frac{1}{{\sqrt 2 }}\)

(D)  \(\frac{3}{4}\)

Với mọi \(\alpha\), \(\sin \left( {\frac{{3\pi }}{2} + \alpha } \right)\) bằng:

(A) sin α

(B) - sin α

(C) - cos α

(D) cos α

\(\frac{{\sin \frac{\pi }{{15}}\cos \frac{\pi }{{10}} + \sin \frac{\pi }{{10}}\cos \frac{\pi }{{15}}}}{{\cos \frac{{2\pi }}{{15}}\cos \frac{\pi }{{15}} - \sin \frac{{2\pi }}{{15}}\sin \frac{\pi }{{15}}}}\) bằng

(A) \(\sqrt 3 \)

(B) 1

(C) - 1

(D) \(\frac{1}{2}\)

\(\cos \frac{\pi }{{12}}\cos \frac{{7\pi }}{{12}}\) bằng

(A) \(\frac{{\sqrt 3 }}{2}\)

(B) \(\frac{{\sqrt 3 }}{4}\)

(C) \(\frac{1}{2}\)

(D) \(-\frac{1}{4}\)

\(\sin \frac{{{{90}^0}}}{4}{\rm{cos}}\frac{{{{270}^0}}}{4}\) bằng:

(A) \(\frac{1}{2}\left( {1 - \frac{{\sqrt 2 }}{2}} \right)\)

(B) \(\frac{1}{2}\left( {\frac{{\sqrt 2 }}{2} - 1} \right)\)

(C) \(\frac{1}{2}\left( {1 + \frac{{\sqrt 2 }}{2}} \right)\)

(D) \(\sqrt 2  - 1\)

\(\frac{{\cos {{80}^0} - \cos {{20}^0}}}{{\sin {{40}^0}\cos {{10}^0} + \sin {{10}^0}\cos {{40}^0}}}\) bằng:

(A) 1

(B) \(\frac{{\sqrt 3 }}{2}\)

(C) - 1

(D) \(-\frac{{\sqrt 3 }}{2}\)

Góc lượng giác (Ou, Ov) có số đo α mà góc uOv là góc nhọn thì:

(A) \(0 \le \alpha  \le \frac{\pi }{2}\)

(B) \( - \frac{\pi }{2} \le \alpha  \le \frac{\pi }{2}\)

(C) \( - \frac{\pi }{2} < \alpha  \le 0\)

(D) Có số nguyên k để \( - \frac{\pi }{2} + k2\pi  < \alpha  < \frac{\pi }{2} + k2\pi \)

Góc lượng giác (Ou, Ov) có số đo α mà góc uOv là góc tù thì:

(A) Có số nguyên k để \(\frac{\pi }{2} + k2\pi  < \alpha  < \frac{{3\pi }}{2} + k2\pi \)

(B) \( - \pi  \le \alpha  \le \frac{{ - \pi }}{2}\)

(C) \( - \frac{\pi }{2}   \le \alpha  \le \frac{{3\pi }}{2}  \)

(D) \(\frac{\pi }{2} < \alpha  \le \pi \)

Với góc lượng giác (OA, OM) có số đo α, xét góc lượng giác (OA, ON) có 1 số đo \(\frac{\alpha }{2}\) (M và N cùng nằm trên đường trọn lượng giác gốc A). Khi đó, với mọi α sao cho M nằm trong góc phần tư thứ III của hệ tọa độ gắn với đường tròn đó (M không nằm trên trục tọa độ), điểm N luôn.

(A) nằm trong góc phần tư I

(B) nằm trong góc phần tư II

(C) nằm trong góc phần tư III

(D) không nằm trong góc phần tư I và III

Với góc lượng giác (OA, OM) có số đo ∝, xét góc lượng giác (OA, ON) có số đo 2∝ (M và N cùng nằm trên đường tròn lượng giác gốc A). Khi đó, với mọi ∝ so cho M nằm trong góc phần tư I của hệ tọa độ gắn với đường tròn đó (M không nằm trên trục tọa độ), điểm N luôn:

(A) nằm trong góc phần tư I

(B) nằm trong góc phần tư II

(C) nằm trong góc phần tư III

(D) không nằm trong góc phần tư IV